×

Warning

Please Login to Read More...

Ratio

Definition: The ratio of two quantities of the same kind in the same units is the fraction that one quantity is of the other. Thus the ratio 'a is to b' is the fraction 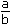written as a : b, here   b ≠ 0. In the ratio "a : b", 'a' is called as the 'first term' or 'antecedent' and 'b' is called as the second term or 'consequent'.

Examples on ratio definitions:

  • The ratio between Rs.50 and Rs.10 is 50 : 10 = 50/10 = 5/1 = 5 : 1
  • The ratio between 5 kg and 15 kg is 5 : 15 = 5/15 = 1/3 = 1 : 3
  • The ratio between Rs.1 and 5 kg is not possible, since they are of different units.

Important property: The value of a ratio remains unchanged, if both of its terms are multiplied or divided by the same non-zero quantity.

Examples on important property:
        5/15 = (5 * 8)/(15 * 8) shows that 5 : 15 is equal to 40 : 120
        3/7 = [3/5]/[7/5] shows that 3 : 7 is equal to 3/5   :   7/5.

Ratio in simplest form: A ratio is said to be in simplest form, if antecedent (first term) and consequent (second term) have no common factors other than one. [It means their HCF is "1"].
Refer to adjacent image for an example.

Compound ratio: If a/b, c/d are two ratios then the compound ratio of a/b and c/d is a/b : c/d = ac/bd = ac : bd. In other words, compound ratio is the ratio of the product of antecedents to the product of consequents of the given ratios.

Example on compound ratio:
        If P : Q = 8 : 6 and Q : R = 6 : 5 then P : Q : R = 8 : 6 : 5.
Another example is given at the adjacent.

Ratios of equality

A ratio x : y = x/y is called a ratio of greater inequality, if x is greater than the y.

A ratio x : y = x/y is called a ratio of less inequality, if x is less than the y.

A ratio x : y = x/y is called a ratio of equality, if x is equal to y.

A ratio of greater inequality (x > y) is reduced (to a lower ratio) by adding the same quantity to both its terms.
If the same quantity is subtracted from both the terms, the ratio of greater inequality is increased.
i.e, x/y > (x + a)/(y + a) and x/y < (x – a)/(y – a)
The converse is true for a ratio of less inequality (x < y).
i.e, x/y < (x + a)/(y + a) and x/y > (x – a)/(y – a)

Comparison of ratios

If a : b = a/b and c : d = c/d are two ratios, then we say that:

 
 
 

Ex: Find the largest and smallest ratios amongst 7/8, 8/9 and 9/10.
Sol: Consider first two ratios: 7/8 and 8/9.
Cross-multiplying we have, 63 ( 7 × 9) < 64 (8 × 8)
So 7/8 < 8/9 ---- (i)
Consider the second and third ratios: 8/9 and 9/10
Again cross-multiplying 80 < 81
So, 8/9 < 9/10 ------ (ii)
From (i) & (ii) we conclude that
9/10 is the largest ratio among the three and
7/8 is the smallest ratio.

Continued ratio: If P : Q and Q : R be two ratios given in such a way that the second term of the first ratio is equal to the first term of the second ratio then we say that P, Q, R are in continued ratio that is P : Q : R.

To divide a quantity in a given ratio

Let us suppose the given quantity is ‘Q’. We have to divide this quantity Q among A, B, C in the ratio p : q : r as follows :

First of all we have to add the ratios, so the sum of the ratios is
s = p + q + r.

1. Share of A = [Q * p/s] = [Quantity * Ratio of A/Sum of the ratios]

2. Share of B = [Q * q/s] = [Quantity * Ratio of B/Sum of the ratios]

3. Share of C = [Q * r/s] = [Quantity * Ratio of C/Sum of the ratios]

Note: The sum of the shares must be equal to the given quantity.

Example: The numbers are in the 9 : 7 ratio. If the difference of their squares is 288 then the smaller of the two numbers is ?
Sol: Let numbers be 9x and 7x
(9x)2 – (7x)2 = 288
81 x2 – 49 x2 = 288
32 x2 = 288

Numbers are 9 x 3 and 7 x 3
∴ 27 and 21
Smaller number is 21

Properties of ratios

1. From the laws of fractions, we know

This implies the ratio a : b is equal to the ratio ma : mb
Therefore the value of a ratio remains unaltered if the antecedent and the consequent are multiplied or divided by the same number.

2. Two or more ratios can be compared by reducing their equivalent fractions to a common denominator.
Let a : b and x : y be two ratios.
We have
Now, the denominators of the two ratios are the same i.e, by.
If ay > bx, the ratio a : b > x : y
If ay < bx, the ratio a : b < x : y

3. The ratio of two fractions can be expressed as a ratio of two integers.
Thus the ratio is measured by a fraction .
It is therefore equivalent to ad : bc

Properties of ratios ....

4. If one or both terms of a ratio is a surd (i.e, an irrational number),
then it cannot be expressed as a ratio of any two integers.
Ex: No two integers can be found to exactly express the ratio √3 : 4.
If the ratio of any two quantities can be expressed exactly as a ratio of two integers,
the quantities are said to be commensurable. Else they are incommensurable.
In the example above, √3 and 4 are incommensurable.
Such quantities can be expressed as a ratio of two integers only to an approximation but never exactly.

5. A ratio compounded with itself is called the duplicate ratio.
So the duplicate ratio of a : b is a2 : b2.
Similarly a3 : b3 is the triplicate ratio of a : b
and a1/2 : b1/2 is the sub-duplicate ratio of a : b.
Ex: (i) The duplicate ratio of 2p : 3q is 4p2 : 9q2
(ii) The sub-duplicate ratio of 81 : 64 is 9 : 8
(iii) The triplicate ratio of 1 : 3b is 1 : 27b3

6. If = ....,
then each of these ratios = ,
where p, q, r, n are any quantities what so ever
When p = q = r = n = 1, we have = ..... =
i.e, when a series of fractions are equal, each of them is equal to sum of all numerators divided by sum of all denominators.

Ratios in multi-disciplines

You very well know that speed is the ratio of distance to time.
i.e,
If distance is measured in km and time in hours, speed has the units km/hr.
π is an irrational number that is approximated by the ratio 22/7.
You will also come across these dimensionless ratios in later classes.

Math

i. In geometry, there are six trigonometric ratios - sine, cosine, tangent, cotangent, secant and cosecant.
In addition, there are six each of inverse trigonometric ratios, hyperbolic trigonometric ratios and inverse hyperbolic trigonometric ratios.
ii. Another ratio of interest is the golden ratio denoted by ϕ.
Two quantities are said to be in golden ratio if their ratio is same as the ratio of their sum to the larger of the two quantities.
i.e, a/b = (a + b)/a
ϕ = 1.61803398875
iii. In statistics, probability of an event is the ratio of number of favourable outcomes to the total outcomes in the sample space of the experiment.

Physics

i. Modulus of elasticity or Young's modulus (Y) of an object is the ratio of tensile stress to tensile strain.
ii. Poisson's ratio (σ) is defined as negative ratio of the lateral strain to the axial strain.
iii. In electronics, amplification factor is the ratio of output of a device to its input.

Chemistry

In chemical reactions, the equilibrium constant (K) is the ratio of the concentration of products to that of the reactions.