Examples
Ex 1:
The exterior angle of a regular polygon is 36° then the polygon is a___
Sol:
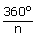 |
= | exterior angle |
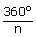 |
= | 36° |
| 36n | = | 360 |
| n | = | 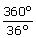 |
| n | = | 10 |
| ∴ The polygon is a decagon. | ||
Ex 2:
Find the regular polygon with an exterior angle equal to the acute angle of a right-angled isosceles triangle.
Sol:
| In an isosceles right-angled triangle, the angles are 45°, 45° & 90°. | ||
| Given that: ext. angle of a polygon | = | acute angle of the Δ |
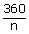 |
= | 45 |
| 45n | = | 360 |
| n | = | 8 (octagon) |
| ∴ The polygon is an octagon. | ||
Ex 3:
Find the measure of each exterior angle of a regular polygon having:
(i) 8 sides
(ii) 9 sides
(iii) 12 sides
Sol:
(i) Each exterior angle of a regular polygon of 8 sides = 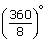 = 45°.
= 45°.
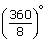 = 45°.
= 45°.(ii) Each exterior angle of a regular polygon of 9 sides = 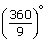 = 40°.
= 40°.
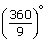 = 40°.
= 40°.(iii) Each exterior angle of a regular polygon of 12 sides = 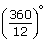 = 30°.
= 30°.
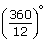 = 30°.
= 30°.Ex 4:
Is it possible to have a regular polygon with an exterior angle of 25° ?
Sol:
Let the number of sides of the given polygon be n.
∴ Each of its exterior angles = 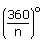
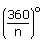
Now, 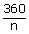 = 25
= 25
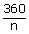 = 25
= 25 ⇒ 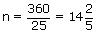 , which is not a whole number.
, which is not a whole number.
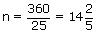 , which is not a whole number.
, which is not a whole number. So, it is impossible to have a regular polygon, each of whose exterior angles is 25°.
Ex 5:
Is it possible to have a regular polygon, each of whose interior angles is 45°?
Sol:
Each interior angle = 45°.
∴ Each exterior angle = (180° – 45°) = 135°
Let the number of sides of the polygon be n.
Then, 135 × n = 360 (∵ sum of all exterior ∠s is 360°)
⇒ 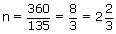 , which is not a whole number.
, which is not a whole number.
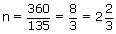 , which is not a whole number.
, which is not a whole number.So, it is impossible to have a regular polygon with an interior angle whose interior angle is 45°.
Ex 6:
Find the measure of each interior angle of a regular
(i) pentagon
(ii) hexagon
(iii) octagon
(iv) polygon of 12 sides
Sol:
(i) Each exterior angle of a regular pentagon = 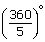 = 72°.
= 72°.
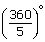 = 72°.
= 72°. ∴ Each of its interior angles = (180° – 72°) = 108°
(ii) Each exterior angle of a regular hexagon = 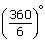 = 60°.
= 60°.
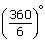 = 60°.
= 60°. ∴ Each of its interior angles = (180° – 60°) = 120°
(iii) Each exterior angle of a regular octagon = 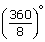 45°.
45°.
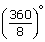 45°.
45°. ∴ Each of its interior angles = (180° – 45°) = 135°
(iv) Each exterior angle of a regular polygon of 12 sides = 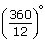 = 30°.
= 30°.
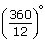 = 30°.
= 30°. ∴ Each of its interior angles = (180° – 30°) = 150°.
Ex 7:
What is the minimum interior angle possible for a regular polygon?
Sol:
As the number of sides of a regular polygon decreases, each exterior angle increases and therefore, each interior angle decreases.
Thus, an equilateral triangle will have minimum interior angle, which is 60°.