Variable force Consider a variable force acting on an object displacing it from position ′a′ to position ′b′ along a curved path as shown. Pulling a spring: When you pull a spring, the force required to pull the spring increases as the spring is stretched. The work done by the force required to stretch the spring is a variable force.

So far we have considered the work done by constant forces only. That is the forces do not vary with the displacement of the object. Quite often the forces we come across in many cases are not constant and they vary in direction or magnitude or both, with the displacement of the object. For example, as a rocket moves away from the earth, work is done to overcome the force of gravity. This gravitational force (F = mg) depends on the distance from the earth′s centre. It varies as the square of the distance from the centre of Earth.

Other examples are the force exerted by a spring during stretching or compressing, which varies with the amount of stretch or compression. The more we stretch a spring, the harder we have to pull, so the force we exert here is not constant. The work done in pulling a box or cart up an uneven hill, is also due to a force that varies with the displacement. We need to be able to compute the work done by forces in such cases.

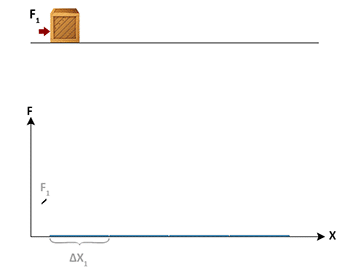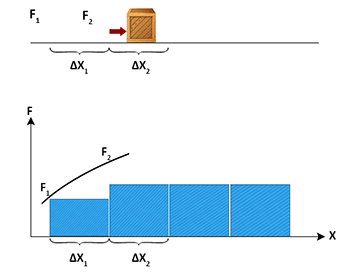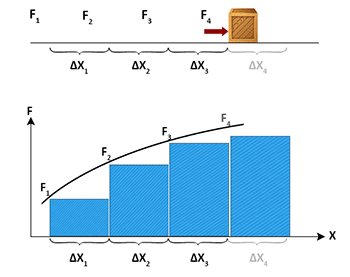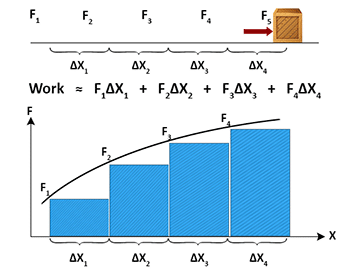
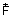Let us divide the path of the object into a large number of infinitesimally small displacements. Each displacement should be so small that force, during that displacement may be regarded as constant. Let dW be the small amount of work done for an infinitesimally small displacement of the object. Let be the corresponding force.

Then,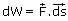

Therefore work done, W = change in the kinetic energy of the body.