Since a string has elastic properties, the disturbance caused on a stretched string at a point, exerts force on neighbouring parts. Neighbouring part responds to this force and this response propagates on the string . Let 'F' be the elastic force in string.
Consider a wave travelling on the string be y = f (t –
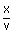 ).
Let us choose an observer who is moving with speed 'V' in positive direction. For the
observer the string does not move in y-direction as the disturbance is also travelling along
with him, with the same speed. If a crest is opposite to him at an instant time(t), it will
always remain opposite to him with the same shape while the string passes through this crest
in opposite direction like a snake.
).
Let us choose an observer who is moving with speed 'V' in positive direction. For the
observer the string does not move in y-direction as the disturbance is also travelling along
with him, with the same speed. If a crest is opposite to him at an instant time(t), it will
always remain opposite to him with the same shape while the string passes through this crest
in opposite direction like a snake.
Consider a small element 'AB' of the string of length 'Δl'
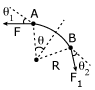
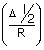
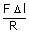 .... (i)
.... (i)This radial force is causing the points on the string slide on the arc AB
with speed 'V'.
Let the mass of an arc 'AB' be 'Δm'.
| ∴ FR | = | 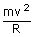 .... (ii) .... (ii) |
| From the equations (i) and (ii), we have | ||
| FR | = | 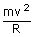 = =
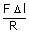 |
| ⇒ v2 | = | 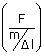 |
Let 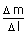 |
= | μ (linear mass density of string) |
| ∴ v | = | 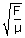 |