Vector area of a triangle

The vector area of Δ ABC is
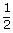 (AB × AC) =
(AB × AC) =
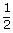 ( BC × BA ) =
( BC × BA ) =
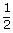 (CA × CB)
(CA × CB)
Proof:
Let n be the unit vector in the direction of AB × AC
Let Δ be the Area of the Δ ABC.
∴ Δ = 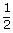 (AB)(AC) sin A
(AB)(AC) sin A
| ∴ The vector area | = | Δ n | |
| = | 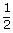 (AB)(AC) (sin A)n (AB)(AC) (sin A)n
| ||
| = | 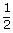 |AB| |AC| (sin A)n |AB| |AC| (sin A)n |
||
| = | 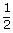 (AB × AC) (AB × AC) |
Similarly, we can prove the vector area = 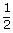 (BC × BA)
=
(BC × BA)
= 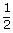 (CA × CB)
(CA × CB)