Variable separable form
  • The method involves obtaining the given differential equation in the form

  • f(x)dx + g(y)dy = 0

  • By integrating each term, we have the solution.
Ex 1:

x dy + 2y dx = 0

Sol:

Dividing by 'xy', the two variables 'x' and 'y' are separated.

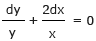
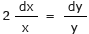
Integrating w.r.t. 'x'

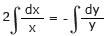
2 log x = – log y + log c
log x2 = log(c/y)
x2 = c/y
x = √(c/y) is the required solution.

Differential Equation reducible to the variable separable type:

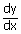  • = f(ax + by + c) a, b ≠ 0

  • To solve this, substitute u = ax + by + c.

  • Then the equation reduces to separable type in the variable 'u' and 'x' which can be solved.
Examples

Ex 1:

Solve 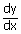= sin(x + y) + cos(x + y).

Sol: Put x + y = u then
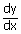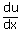= – 1 ------ (i)
The given eqn. (i) transforms to
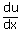– 1 = sin u + cos u
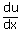⇒ = 1 + sin u + cos u
Separating the variable and integrating we get

Ex 2:

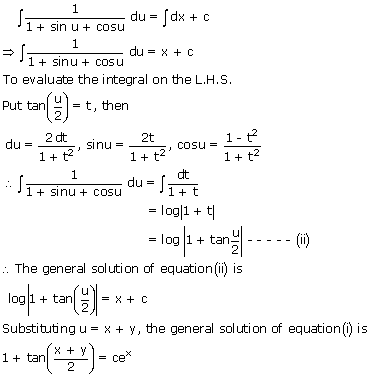
Solve (x – y)2 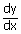= a2

Sol:

Put x – y = u then

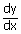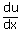= 1 – ---- (i)

∴ Eqn. (i) transform to u2(1 – 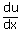) = a2

Ex 3:

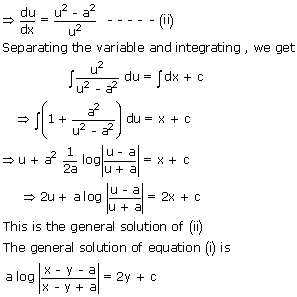
Solve y dx – x dy + 4x3 y2 ex4 dx = 0.

Sol:

The given differential equation can be written as

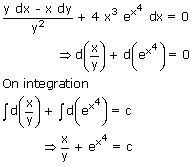
This is in general solution of the given D.E.