Examples
Ex 1:
Prove that each angle of an equilateral triangle is 60°.
Proof
Let the given triangle is ΔPQR.
| PQ | = | QR = PR |
| Prove that ∠P | = | ∠Q = ∠R = 60° |
| PQ | = | QR |
| ∠P | = | ∠R (∵ Angles opposite to equal sides are equal) |
| PQ | = | PR |
| ⇒ ∠Q | = | ∠R |
| ⇒ ∠P | = | ∠Q = ∠R |
| Since ∠P + ∠Q + ∠R | = | 180° |
| ⇒ ∠P + ∠P + ∠P | = | 180° |
| ⇒ 3 ∠P | = | 180° |
| ⇒ ∠P | = | 60° |
| ∴ ∠P = ∠Q = ∠R | = | 60° |
Ex 2:
PQR is a right angled triangle in which ∠P = 90° and PQ = PR. Find ∠Q and ∠R

Sol:
| Given that PQ = PR | ||
| ∠R | = | ∠Q |
| (angles opposite to equal sides are also equal) In ΔPQR |
||
| ∠P + ∠Q + ∠R | = | 180° |
| (Angle sum property of a triangle) | ||
| 90° + ∠Q + ∠R | = | 180° |
| 90° + ∠Q + ∠Q | = | 180° |
| 2∠Q | = | 90° |
| ∠Q | = | 45° |
| ∴ ∠Q | = | ∠R = 45° |
Ex 3:
If the bisector of the vertical angle of a triangle bisects the base, prove that the triangle is isosceles.
Sol:
Given a ΔABC in which AD is the bisector of ∠A which meets BC at D such that BD = DC.
To prove: AB = AC
Construction: AD to E such that AD = DE join EC.
Proof:
In triangle ABD and ECD, we have:
| BD | = | DC (given) |
| AD | = | DE (by construction) |
| ∠ADB | = | ∠EDC (vertically opposite angles) |
| ∴ ΔABD | ≅ | ΔECD |
| ∴ AB | = | EC and ∠1 = ∠3 (c.p.c.t) |
| Also, ∠1 | = | ∠2 [∵ AD bisects ∠ A] |
| ∴ ∠2 | = | ∠3 |
| Consequently, EC | = | AC [sides opp. to equal angles] |
| ∴ AB | = | AC [∵ EC = AB] |
| Hence, ΔABC is isosceles. |
Ex 4:
In an isosceles triangle PQR, with PQ = PR, the bisectors of ∠Q and ∠R intersect each other at O. Join P to O. Show that
(i) OQ = OR
(ii) PO bisects ∠P
Sol:
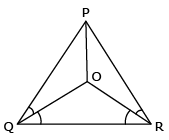
| (i) It is given that in triangle PQR, PR = PQ | ||
| ∠PRQ | = | ∠PQR |
| angles opposite to equal sides of a triangle are equal | ||
 ∠PRQ ∠PRQ |
= |  ∠PQR ∠PQR |
| ∠ORQ | = | ∠OQR |
| OQ | = | OR |
| (Sides opposite to equal angles of a triangle are also equal) | ||
| (ii) Now in ΔOPQ and ΔOPR | ||
| PO | = | PO (Common) |
| PQ | = | PR |
| OQ | = | OR |
| So, ΔOPQ | ≅ | ΔOPR (by SSS congruence rule) |
| ∠QPO | = | ∠RPO (by CPCT) |
Ex 5:
PQR and SQR are two isosceles triangles on the same base QR. Show that ∠PQS = ∠PRS

Sol:
| Let us join PS In ΔPQS and ΔPRS |
||
| PQ | = | PR |
| QS | = | RS |
| PS | = | PS (Common side) |
| ∴ ΔPQS | ≅ | ΔPRS (by SSS congruence rule) |
| ∠PQS | = | ∠PRS |