Example
Ex 1:
In an isosceles triangle, prove that the altitude from the vertex bisects the base.
Sol:
Given A ΔABC in which AB = AC and AD ⊥ BC.
To prove: BD = DC.
Proof:
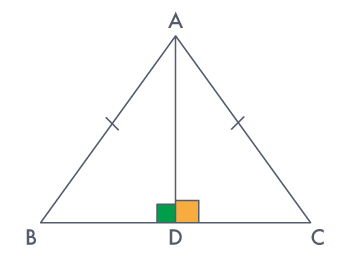
In right-angled ΔADB and ADC, we have
| hyp. AB | = | hyp.AC (Given) |
| AD | = | AD (Common) |
| ∴ ΔADB | ≅ | ΔADC [RHS-Criteria] |
| Hence, BD | = | DC (c.p.c.t) |
Ex 2:
If the altitude from one vertex of a triangle bisects the opposite side, prove that the triangle is isosceles.
Sol:
Given A ΔABC in which AD ⊥BC and BD = DC.
To prove: AB = AC.
Proof:
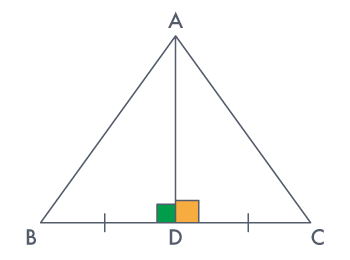
In ΔADB and ADC, we have:
| BD | = | DC(Given) |
| AD | = | AD (common) |
| ∠ADB | = | ∠ADC = 90° |
| ∴ ΔADB | ≅ | ΔADC (SAS-criteria) |
| Hence, AB | = | AC (c.p.c.t) |