EXAMPLES
Ex 1:
What could be the least number which, when we divide by 20, 25 and 30, leaves a remainder of 6 in every case?
Sol:
As we have to find the least number, we will calculate the LCM first.
LCM of 20, 25 and 30.
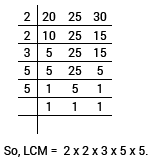
LCM of 20, 25 and 30 is 2 × 2 × 3 × 5 × 5 = 300.
Here 300 is the least number divided by 20, 25 and 30, which will leave the remainder of 0 in each case.
But we have to find the least number, which leaves the remainder 6 in all cases.
Hence, the required number is 6, more than 300.
The required least number = 300 + 6 = 306.
Ex 2:
For each of the following pairs of numbers, verify the property:
Product of numbers = Product of their H.C.F. and L.C.M.
(i) 14, 21
(ii) 27, 90
Sol:
(i) We compute the H.C.F and L.C.M. of 14 and 21 as under:
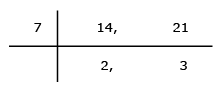
∴ H.C.F. of 14 and 21 is 7 and,
L.C.M. = 7 × 2 × 3 = 42.
Now, H.C.F. × L.C.M. = 7 × 42 = 294
Product of numbers = 14 × 21 = 294
∴ Product of the numbers = Product of their H.C.F. and L.C.M.
(ii) We compute the H.C.F. and L.C.M. of 27 and 90 as under:
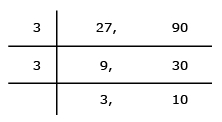
∴ H.C.F. = 3 × 3 = 9 and
L.C.M. = 3 × 3 × 3 × 10 = 270.
Now, H.C.F. × L.C.M. = 9 × 270 = 2430
Product of numbers = 27 × 90 = 2430
Hence, the product of numbers = H.C.F. × L.C.M.
Ex 3:
Given that the H.C.F. of two numbers is 16 and their product is 6400, determine their L.C.M.
Sol:
We know that:
H.C.F. × L.C.M = product of numbers.

Here, H.C.F. = 16 and Product of numbers = 6400.
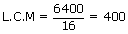
Ex 4:
The H.C.F. and L.C.M. of the two numbers are 13 and 1989, respectively. If one of the numbers is 117, determine the other.
Sol:
We know that: (One number) × (The other number) = H.C.F. × L.C.M.
Here, H.C.F. = 13
L.C.M. = 1989 and
One number = 117
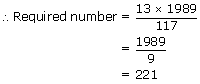
Ex 5:
Can two number have 14 as their H.C.F and 204 as their L.C.M. Give reasons to support your answer.
Sol:
We know that the H.C.F. of given numbers must divide their L.C.M exactly.
But 14 does not divide 204 exactly.
So, there can be no two numbers with 14 as their H.C.F. and 204 as their L.C.M.