We know the wave equation is of the form
).
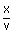A very important special case when the source (at x = 0) vibrates in a simple harmonic motion.
Let source disturbance f(t) = A sin (ωt + ϕ)
Where 'A' represents the amplitude and 'ω' represents angular frequency. The time period of
oscillation is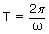 
and frequency of
oscillation is ν =
.
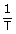Such a sinusoidal source disturbance produces sinusoidal wave.
| Since f(t) | = | A sin (ωt + ϕ), then the wave equation caused by it is |
| y | = | f(t – ) |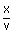
| y | = | A sin ω(t – +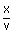
ϕ) |
| y | = | A sin (ωt – 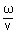 x +
ϕ) |
| Let |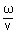
= | k, k is called wave number |
| ∴ y | = | A sin (ωt – kx + ϕ) |
Each particle copies the motion of another particle at its left with a
time delay of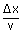 
where 'Δx' is the separation between both the points.
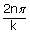) + ϕ)⇒ At any time 't' all points on x-axis.
Which are of the form x –
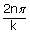have the same displacement and same velocity and identical to each other in all respects.
| ⇒ Shortest distance between such two points | = | x – (x –  ) |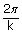
| = |
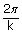(when n = 1) |
Which is called wavelength of the wave.
∴ λ = 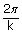( k is a wave number)