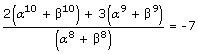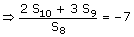quadratic_examples

Examples

1. The equation ax² + bx + c = 0 (a ≠ 0) possesses exactly two roots But if the equation ax² + bx + c = 0 is satisfied by more than two distinct values of 'x' then it is called an Identity and we have a = 0, b = 0, c = 0

Proof:

α, β, γ(α ≠ β ≠ γ) are roots of ax² + bx + c

⇒ aα² + bα + c = 0 . . . . .(I)

aβ² + bβ + c = 0 . . . . . .(II)

aγ² + bγ + c = 0 . . . . . (III)

(I) – (II) ⇒ a(α + β) + b = 0 . . . . . (IV)

(II) – (III) ⇒ a(β + γ) + b = 0 . . . . .(V)

(IV) – (V); a( α – γ) = 0 ⇒ a = 0 (∵ α ≠ γ)

From(IV); b = 0⇒ c = 0

∴ ax² + bx + c = 0 is an Identity

i.e., possesses Infinite solutions ⇔ a = b = c = 0

2. The equation ax² + bx + c = 0 has

(i) One root Infinity, when a = 0, b ≠ 0

(ii) Two Roots are Infinity, when a = b = 0, c ≠ 0

Proof:

EX 1:

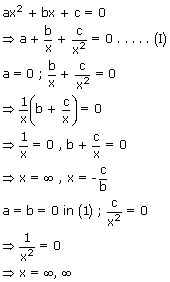
Find the value of P for which the equation (R³ – 3R² + 2R)x² + (R³ – R)x + R³ + 3R² + 2R = 0

(i) Becomes an identity

(ii) Has exactly one root at infinity

(iii) Has both the roots at infinity

Sol:

(i) Equation becomes an identity

a = 0 b = 0 c = 0

R = 0, 1, 2; R = 0, ± 1; R = – 1, – 2, 0

Hence R = 0

(ii) Equation has exactly one root at infinity

a = 0, b ≠ 0

R = 0, 1, 2; R ≠ ± 1, 0

Hence R = 2

(iii) Equation has both the roots at infinity

a = 0 b = 0 c ≠ 0

R = 0, 1, 2; R = ± 1, 0 R ≠ – 1, – 2, 0

Hence R = 1

3. Let α, β are the Roots of Quadratic Equation ax² + bx + c = 0 then we have the identity in 'n'. Say a.S_n + b.S_{n – 1} + c.S_{n – 2} = 0 Where

S_n = αⁿ + βⁿ, S_{n – 1} = α^{n – 1} + β^{n – 1}, S_{n – 2} = α^{n – 2} + β^{n – 2}

Proof:

Given that

α, β are roots of ax² + bx + c = 0

⇒ aα² + bα + c = 0, aβ² + bβ + c = 0

⇒ α^{n – 2}(aα² + bα + c) = 0, β^{n – 2}(aβ² + bβ + c) = 0

⇒ aαⁿ + bα^{n – 1} + cα^{n – 2} = 0, aβⁿ + bβ^{n – 1} + cβ^{n – 2} = 0

Add this two equation

⇒ a(αⁿ + βⁿ) + b(α^{n – 1} + β^{n – 1}) + c(α^{n – 2} + β^{n – 2}) = 0

⇒ aS_n + b S_{n –1} + c S_{n – 2} =

Ex 1:

α, β are Roots of 2x² + 3x + 7 = 0, then

Sol:

2S₁₀ + 3.S₉ + 7 S₈ = 0

⇒ 2S₁₀ + 3.S₉ = – 7S₈