Examples
Ex 1:
Intercept Theorem: If there are three parallel lines and the intercepts made by them on one transversal are equal then the intercepts on any other transversal are also equal.
Sol:
Given Three parallel lines l, m and n are cut by a transversal p at A, B, and C respectively such that AB = BC.
Also, q is another transversal, cutting l, m, and n at P, Q, and R respectively.
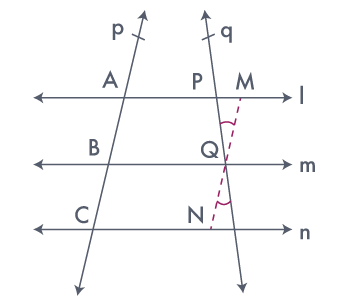
To prove : PQ = QR
Construction : Through Q, draw a line segment parallel to transversal p, meeting l, m, n, At M, Q and N respectively.
AM ∥ BQ [∵ l ∥ m]
MQ ∥ AB [By construction]
∴ ABQM is a parallelogram
∴ MQ = AB ––––– (i)
Similarly, CNQB is a parallelogram
∴ NQ = BC –––––– (ii)
But, AB = BC
∴ MQ = NQ [from (i) and (ii)]
Now, in Δ MPQ and NRQ, we have: MQ = NQ (proved).
∠ MQP = ∠NQR (vert.opp.∠s)
∠PMQ = ∠RNQ [Alt.Int.∠s]
∴ Δ MPQ ≅ Δ NRQ
∴ PQ = QR (c.p.c.t)
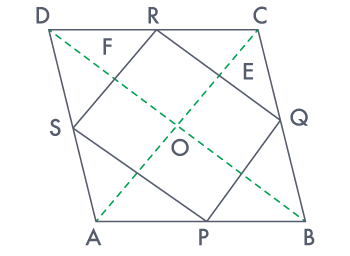
Ex 2:
ABCD is a rhombus and P, Q, R and S are the mid–points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Sol:
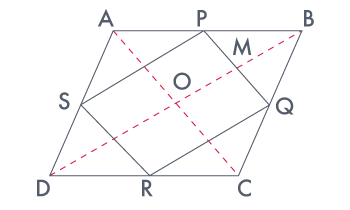
Given in the question,
ABCD is a rhombus and P, Q, R and S are the mid–points of the sides AB, BC, CD and DA, respectively.
To Prove : PQRS is a rectangle.
Construction :Join AC and BD.
Proof:
In ΔDRS and ΔBPQ,
DS = BQ (Halves of the opposite sides of the rhombus)
∠SDR = ∠QBP (Opposite angles of the rhombus)
DR = BP (Halves of the opposite sides of the rhombus)
ΔDRS ≅ ΔBPQ [SAS congruency]
RS = PQ [CPCT]–––––––– (i)
In ΔQCR and ΔSAP,
RC = PA (Halves of the opposite sides of the rhombus)
∠RCQ = ∠PAS (Opposite angles of the rhombus)
CQ = AS (Halves of the opposite sides of the rhombus)
ΔQCR ≅ ΔSAP [SAS congruency]
RQ = SP [CPCT]–––––––– (ii)
Now,
In ΔCDB,
R and Q are the mid points of CD and BC, respectively.
⇒ QR ∥ BD
also,
P and S are the mid points of AD and AB, respectively.
⇒ PS ∥ BD
⇒ QR ∥ PS
PQRS is a parallelogram.
also, ∠PQR = 90°
Now,
In PQRS,
RS = PQ and RQ = SP from (i) and (ii)
∠Q = 90°
PQRS is a rectangle.
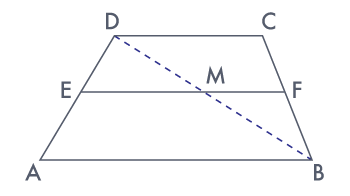
Ex 3:
PQRS is a trapezium in which PQ ∥ SR, SQ is diagonal and A is the mid–point of PS. A line is drawn through A parallel to PQ intersecting BC at F. Show that B is the mid–point of RQ.
Sol:
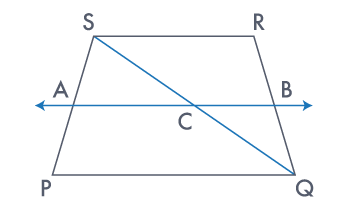
Let AB intersect SQ at C.
By converse of a mid–point theorem,
we know that a line drawn through the mid–point of any side of a triangle and parallel to another side bisects the third side.
In ΔPSQ,
AB ∥ PQ and A are the mid–point of PS
Therefore, C is the mid–point of SQ
AS AB ∥ PQ and PQ ∥ SR,
∴ AB ∥ SR (two lines parallel to the same line are parallel to each other)
In ΔQRS, CB ∥ SR and C are the mid–point of line QS
Therefore, by using the converse of the mid–point theorem, B is the mid–point of QR.
Ex 4:
Let ABCD be a trapezium in which AB ∥ DC and let E be the midpoint of AD. Let F be a point on BC such that EF ∥ AB. Prove that
(i) F is the midpoint of BC
(ii) EF = (AB + DC)
Sol:
Join BD, cutting EF at M.
Now, in Δ DAB, E is the midpoint of AD and EM ∥ AB.
∴ M is the midpoint of BD.
∴ EM = AB ––––– (i)
Again, in ΔBDC, M is the midpoint of BD and MF ∥ DC.
∴ F is the midpoint of BC
∴ MF = DC ––––– (ii)
∴ EF = EM + MF = (AB + DC) [from (i) and (ii)]
Hence, F is the midpoint of BC and EF = (AB + DC).
Ex 5:
Show that the quadrilateral formed by joining the midpoints of the pairs of adjacent sides of a rectangle is a rhombus.
Sol:
Let ABCD be a rectangle and P, Q, R, and S be the midpoints of AB, BC, CD and DA respectively.
Clearly, PQRS is a parallelogram.
Now, ΔSAP ≅ ΔQBP
[∵ AS = BQ, ∠A = ∠B = 90° and AP = BP]
⇒ PS = PQ (by CPCT)
⇒ RQ = PS = PQ = RS.
Hence, PQRS is a rhombus.
Ex 6:
Show that the quadrilateral formed by joining the midpoints of the pairs of adjacent sides of a rhombus is a rectangle.
Sol:
Let ABCD be a rhombus and P, Q, R, and S be the midpoint of AB, BC, CD and DA respectively.
Then, PQRS is parallelogram [prove it].
Diagonals of a rhombus bisect each other at right angles.
∴ ∠EOF = 90°
Now, RQ ∥ DB ⇒ RE ∥ FO, SR ∥ AC ⇒ FR ∥ OE.
∴ OERF is a ∥gm. So, ∠FRE = ∠EOF = 90°
Thus, PQRS is a ∥gm with ∠R = 90°.
Hence, PQRS is a rectangle.