Displacement relation in a progressive wave
Let us consider a sinusoidal travelling wave. For convenience, we shall take the wave to be transverse so that if the position of the constituents (particles) of the medium is denoted by x, the displacement from the equilibrium position may be denoted by y. A sinusoidal travelling wave is then described by:

y = a sin(kx – ωt + ϕ)---------------(1)

Where
y is the displacement of the particle from the equilibrium position
a is the amplitude of a wave
ω is the angular frequency of the wave
k is the angular wave number
(kx – ωt + ϕ) is the initial phase angle

The term ϕ in the equation means that we are considering a linear combination of sine and cosine functions:

y = A sin(kx – ωt) + B cos(kx – ωt)--------------- (2)

From Equations (1) and (2),

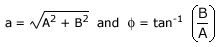
To understand why Equation (1) represents a sinusoidal travelling wave, let us consider a fixed instant, say t = t0 (i.e. t = 0). Then the the sine function in Equation (1) is simply kx + constant. Thus the shape of the wave (at any fixed instant) is a sine wave. Similarly, let us consider a fixed location, say x = x0 (i.e. x = 0). Then the sine function in Equation (1) is constant -ωt. The displacement y, at a fixed location, thus varies sinusoidally with time. That is, the particles of the medium at different positions execute simple harmonic motion. Finally, as t increases, x must increase in the positive direction to keep kx – ωt + ϕ constant. Thus Eq. (1) represents a sinusiodal (harmonic) wave travelling along the positive direction of the x-axis. On the other hand, the equation for a wave travelling in the negative direction is given as

y = a sin(kx + ωt + ϕ)-----------------(3)

Fig. I shows the plots of Eq. (1) for different values of time differing by equal intervals of time. In a wave, the crest is the point of maximum positive displacement, the trough is the point of maximum negative displacement. To see how a wave travels, we can fix attention on a crest and see how it progresses with time. In the figure, this is shown by a cross (x) on the crest. In the same manner, we can see the motion of a particular constituent of the medium at a fixed location, say at the origin of the x-axis. This is shown by a solid dot (•) The plots of Fig. I show that with time, the solid dot (•) at the origin moves periodically i.e. the particle at the origin oscillates about its mean position as the wave progresses. This is true for any other location also. We also see that during the time the solid dot (•) has completed one full oscillation, the crest has moved further by a certain distance. Using the plots of Fig. I, we now define the various quantities of Eq. (1).

Fig I:
Amplitude and Phase:

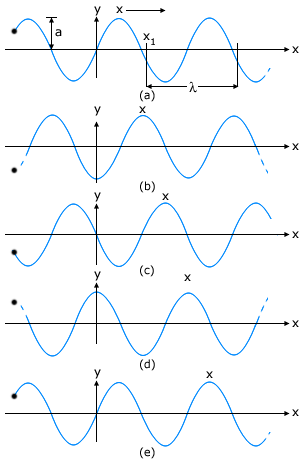
In Eq. (1), since the sine function varies between 1 and -1, the displacement 'y' varies between 'a' and '-a'. We can take 'a' to be a positive constant. Then 'a' represents the maximum displacement of the constituents of the medium from their equilibrium position. Note that the displacement 'y' may be positive or negative, but 'a' is positive. It is called the amplitude of the wave.

The quantity (kx - at + ϕ) in Eq. (1) is called the phase of the wave. Given the amplitude 'a', the phase determines the displacement of the wave at any position and at any instant. Clearly ϕ is the phase at x = 0 and t = 0. Hence ϕ is called the initial phase angle. By suitable choice of origin on the x-axis and the initial time, it is possible to have ϕ = 0.
Wavelength and Angular Wave Number:

The minimum distance between two points having the same phase is called the wave length of the wave, usually denoted by X. For simplicity, we can choose points of the same phase to be crests or troughs. The wavelength is then the distance between two consecutive crests or troughs in a wave. Taking ϕ = 0 in Eq. (1), the displacement at t = 0 is given by

y = a sin kx -------------- (4)

Since the sine function repeats its value after every 2π change in angle,

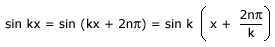
That is the displacements at points x and at 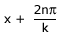are the same, where n = 1, 2, 3, . . . The least distance between points with the same displacement (at any given instant of time) is obtained by taking n = 1. λ is then given by

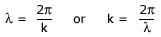--------------(5)

k is the angular wave number or propagation constant; its SI unit is radian per metre or rad m-1.

Period, Angular frequency and Frequency:

Fig. II shows again a sinusoidal plot. It describes not the shape of the wave at a certain instant but the displacement of a particle (at any fixed location). We may for, simplicity, take Eq. (1) with ϕ = 0 and monitor the motion of the particle say at x = 0. We then get

Fig II:
y = a sin(-ωt)
=-a sin(ωt)

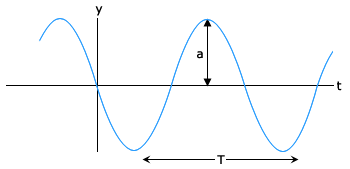
Now the period of oscillation of the wave is the time it takes for a particle to complete one full oscillation. That is

-a sin cot = -a sin ω(t + T)
= -a sin(ωt + ωT)
Since sine function repeats after every 2π.

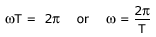---------(6)

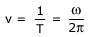ω is called the angular frequency of the wave. Its SI units is rad s-1. The frequency ν is the number of oscillations per second. Therefore,

---------(7)

ν is usually measured in hertz.

In the discussion above, reference has always been made to a wave travelling along a string or a transverse wave. In a longitudinal wave, the displacement of a particle of the medium is parallel to the direction of propagation of the wave. In Eq. (1), the displacement for a longitudinal wave is written as,

s = a sin [kx- ωt + π] ---------------- (8)

where 's' is the displacement of a particle in the direction of propagation of the wave at position 'x' and time 't'. In Eq. (8), 'a' is the displacement amplitude; other quantities have the same meaning as in case of a transverse wave except that the displacement 'y' is to be replaced by 's'.