There are n objects out of which 'p' objects are of 'A' type and all 'A' type objects are alike.

There are q 'alike objects' which are of 'B' type and there are r 'alike objects' which are of 'C' type.

Initially consider all 'n' objects to be different.

So there are 'n!' arrangements possible. Take any one arrangement out of these n! arrangements.

In this particular arrangement permute only 'A' type objects among themselves without altering other objects.

The permutation among 'A' type objects can be done in p! ways. If these 'p' objects are all alike, all of p! arrangements are equivalent to one arrangement.

Hence n! arrangement get reduced to 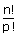arrangements if 'p' objects are alike.

By the same argument these 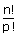arrangements becomes if 'q' other objects are alike.

The argument can be extended to any number of 'Alike objects'.