Examples
Ex1:
The water tax bills (in rupees) of 30 houses in a
locality are given below. Construct a grouped frequency distribution with a class size of
10.
30, 32, 45, 54, 74, 78, 108, 112, 66, 76, 88, 40, 14, 20, 15, 35, 44, 66, 75, 84,
95, 96, 102, 110, 88, 74, 112, 14, 34, 44.
Sol:
Here the maximum and minimum values of the variate
are 112 and 14 respectively
∴ Range = 112 – 14 = 98
It is given that the class size is 10, and
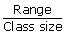 =
98/10 = 9.8
=
98/10 = 9.8So, we should have 10 classes each of size 10
The minimum and maximum values of the variates are 14 and 112 respectively. So, we
have to make the classes in such a way that the first class includes the minimum value and
the last class includes the maximum value.
If we take the first class as 14-24 it
includes the minimum value of 14.
If the last
class is taken as 104 – 114, then it includes the maximum value of 112.
Here, we
form classes by exclusive method.
In classes 14 – 24, 14 is included but 24 is
excluded.
Similarly, in other classes, the lower limit is included and the upper limit
is excluded.
In view of the above discussion, we construct the frequency distribution table as follows:
| Bill (in Rs.) | Tally marks | Frequency |
|---|---|---|
| 14 – 24 | |||| | 4 |
| 24 – 34 | || | 2 |
| 34 – 44 | ||| | 3 |
| 44 – 54 | ||| | 3 |
| 54 – 64 | | | 1 |
| 64 – 74 | || | 2 |
| 74 – 84 | 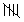 |
5 |
| 84 – 94 | ||| | 3 |
| 94 – 104 | ||| | 3 |
| 104 – 114 | |||| | 4 |
| Total | 30 |
Ex2:
The weights in grams of 50 apples picked at random
from a consignment are as follows:
131, 113, 82, 75, 204, 81, 84, 118, 104, 110, 80, 107,
111, 141, 136, 123, 90, 78, 90, 115, 110, 98, 106, 99, 107, 84, 76, 186, 82, 100, 109, 128,
115, 107, 115, 119, 93, 187, 139, 129, 130, 68, 195, 123, 125, 111, 92, 86, 70,
126.
Form the grouped frequency table by dividing the variable range into intervals of
equal width of 20g, such that the mid-value of the first class interval is 70g.
Sol:
Size of each class = 20
Let the lower limits of the first-class interval be 'a'.
Then, its upper limit = (a + 20)
Mid-value of the first class interval = 70
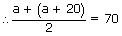
⇒ 2a = 120
⇒ a = 60
∴ The first-class interval is 60 – 80.
So, we may give the frequency distribution as under.
| Weight (in grams) | Tally marks | Frequency |
|---|---|---|
| 60 –80 | 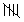 |
5 |
| 80 – 100 | 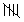 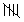 ||| ||| |
13 |
| 100 – 120 | 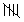 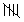 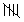 || || |
17 |
| 120 – 140 | 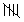 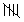 |
10 |
| 140 – 160 | | | 1 |
| 160 – 180 | 0 | |
| 180 – 200 | ||| | 3 |
| 200 – 220 | | | 1 |
| Total | 50 |
Ex3:
The class marks of distribution are:
47, 52, 57,
62, 67, 72, 77, 82, 87, 92, 97, 102.
Determine the class size, the class limits, and
the true class limits.
Sol:
Here the class marks are uniformly spaced. So, the
class size is the difference between any two consecutive class marks.
∴ Class
size = 52 – 47 = 5
We know that, if a is the class mark of a class interval and h
is its class size, then the lower and upper limits of the class interval are a – 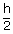 and
a +
and
a + 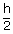 respectively.
respectively.
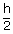 and
a +
and
a + 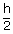 respectively.
respectively.| ∴ The lower limit of first-class interval | = | 47 – 5/2 |
| = | 44.5 | |
| The upper limit of first-class interval | = | 47 + 5/2 |
| = | 49.5 | |
| So, the first class interval is 44.5 – 49.5. | ||
Similarly, we obtain the other class limits as given under:
| Class marks | Class limits |
|---|---|
| 47 | 44.5 – 49.5 |
| 52 | 49.5 – 54.5 |
| 57 | 54.5–59.5 |
| 62 | 59.5 – 64.5 |
| 67 | 64.5 – 69.5 |
| 72 | 69.5 – 74.5 |
| 77 | 74.5 – 79.5 |
| 82 | 79.5 – 84.5 |
| 87 | 84.5 – 89.5 |
| 92 | 89.5 – 94.5 |
| 97 | 94.5 – 99.5 |
| 102 | 99.5 – 104.5 |
Since the classes are exclusive, so the true class limits are the same as
the class limits.