Examples
Ex 1:
Find the H.C.F. and L.C.M. of 30, 12 and 2 by the prime factorisation method.
Sol:
| 30 | = | 2 × 3 × 5 |
| 12 | = | 2 × 2× 3 |
| 2 | = | 2 × 1 |
| H.C.F. | = | 2 |
| L.C.M. | = | 22 × 3 × 5 = 60 |
Ex 2:
Explain why 3 × 5 × 7 + 7 is a composite number.
Sol:
The numbers are not prime numbers having factors other than
one are known as composite numbers.
Now we have 3 × 5 × 7 + 7
We can write as by considering 7 as a common factor of two terms
= 7(3 × 5 + 1)
= 7(15 + 1)
= 7(16) = 112
So, factors are 7 × 4 × 4 which has a value equal to 112 and has more than one
factor. So, it is a composite number.
Ex 3:
Find the H.C.F. and L.C.M. of 60, 84 and 108 using the prime factorisation method.
Sol:
We have
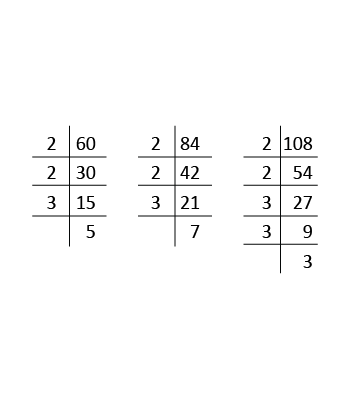
| 60 | = | (22 × 3 × 5) |
| 84 | = | (22 × 3 × 7) |
| 108 | = | (22 × 33) |
| ∴ H.C.F. (60, 84, 108) | = | (22 × 3) |
| = | 12 | |
| L.C.M. (60, 84, 108) | = | (22 × 33 × 5 × 7) |
| = | 3780 |
Ex 4:
Find the largest number which divides 546 and 764,
leaving the remainder 6 and 8 respectively.
Sol:
The required number
divides (546 – 6) i.e., 540 and (764 – 8), i.e., 756 exactly.
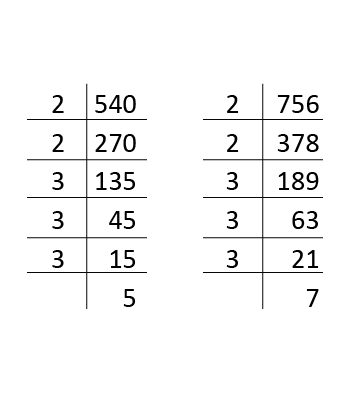
| Now, 540 | = | (22 × 33 × 5) |
| and 756 | = | (22 × 33 × 7) |
| ∴ H.C.F. (540, 756) | = | (22 × 33) |
| = | (4 × 27) | |
| = | 108 | |
| Hence, the required number is 108. | ||