Examples
Ex 1:
One side of a triangle is produced and the exterior angle so formed is 120°. If the interior
opposite angles are in the ratio 3 : 5. Find the measure of each angle of the triangle.
Sol:
Let the given interior opposite angles be (3x)° and (5x)°.
We know that an exterior angle of a triangle is equal to the sum of its interior opposite angles.
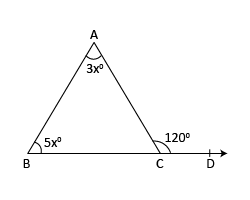
| 3x + 5x | = | 120 |
| 8x | = | 120 |
| x | = | 15 |
| ∠A | = | (3 × 15)° = 45° |
| ∠B | = | (5 × 15)° = 75° |
| But, ∠A + ∠B + ∠C | = | 180° |
| 45° + 75° + ∠C | = | 180° |
| 120° + ∠C | = | 180° |
| ∠C | = | 180° – 120° = 60° |
| ∴ ∠A | = | 45°, ∠B = 75° and ∠C = 60° |
Ex 2:
If the sides of a triangle are produced in order, prove that the sum of the exterior angles so formed is
360°.
Sol:
Let the sides BC, CA and AB of ΔABC be produced to D, E and F respectively, as shown in the figure.
We know that an exterior angle of a triangle is equal to the sum of its interior opposite angles.
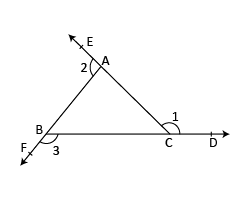
| ∠1 | = | ∠A + ∠B ------- (i) |
| ∠2 | = | ∠B + ∠C ------- (ii) |
| ∠3 | = | ∠C + ∠A ------- (iii) |
On adding the corresponding sides of (i), (ii) and (iii), we get
| ∠1 + ∠2 + ∠3 | = | 2(∠A + ∠B + ∠C) |
| = | 2 × 180° (∵ sum of the angles of a triangle is 180°) | |
| = | 360° | |
| ∴ ∠1 + ∠2 + ∠3 | = | 360° |
Hence, the sum of the exterior angles is 360°.
Ex 3:
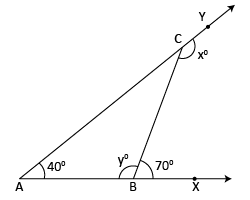
In the figure, the measures of some of the angles are indicated. Find the value of x° and y°.

Sol:
In ΔABC, exterior ∠CBX at B and adjacent interior ∠CBA form a linear pair.
∴ ∠CBX + ∠CBA = 180°
⇒ 70° + y° = 180°
⇒ y° = 180° – 70° = 110°
⇒ y° = 110°
Again, ∠BCY is the exterior of ΔABC at C, and ∠CAB and ∠CBA are interior opposite angles.
∠BCY = ∠CAB + ∠CBA
⇒ x° = 40° + y°
⇒ x° = 40° + 110° (∵ y° = 110°)
⇒ x° = 150°
Hence, we have x° = 150° and y° = 110°.
Ex 4:
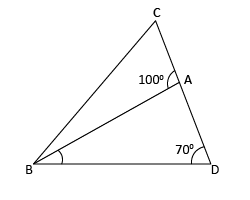
In the figure, find ∠ABD. Also, if ∠C = 3∠ABC, find ∠ABC.

Sol:
In ΔABD, exterior ∠BAC at A and adjacent interior ∠BAD form a linear pair.
∠BAD + ∠BAC = 180°
∠BAD + 100° = 180°
∠BAD = 180° – 100°
∠BAD = 80°
In ΔABD, the sum of the angles is 180°.
∠ABD + ∠BAD + ∠ADB = 180°
∠ABD + 80° + 70° = 180°
∠ABD + 150° = 180°
∠ABD = 180° – 150°
∠ABD = 30°
Again, in ΔABC, we have
∠ABC + ∠C + ∠BAC = 180°
∠ABC + 3∠ABC + 100° = 180° (∵ C = 3∠ABC (given))
4∠ABC = 180° – 100°
4∠ABC = 80°
∠ABC = 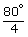 = 20°
= 20°
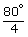 = 20°
= 20°