1. Draw a polygon (a pentagon ABCDE as shown in figure) on the floor using a piece of chalk.

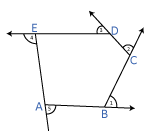
2. Start walking from A. Walk along AB on reaching B, you need to turn through an angle of m∠1 to walk along BC. On reaching C, you must turn through an angle of m∠2 to walk along CD.

3. Continue moving in the same manner,until you return to the side AB.

4. You will find that you have made one complete turn.

Therefore, m∠1 + m∠2 + m∠3 + m∠4 + m∠5 = 360°.

Hence, the sum of the,measures of the exterior angles of a pentagon is 360°. This is true for every polygon.