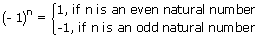We have
| 100 | = | 10 ⨯ 10 |
| 1000 | = | 10 ⨯ 10 ⨯ 10 |
| 10000 | = | 10 ⨯ 10 ⨯ 10 ⨯ 10 |
| 100000 | = | 10 ⨯ 10 ⨯ 10 ⨯ 10 ⨯ 10 |
So, the exponential forms of 100, 1000, 10000 and 100000 are as given below:
| 100 | = | 102 (read as 10 raised to the power 2) |
| 1000 | = | 103 (read as 10 raised to the power 3) |
| 10000 | = | 104 (read as 10 raised to the power 4) |
| 100000 | = | 10 5 (read as 10 raised to the power 5) |
Some powers have special names. For example,
52, which is 5 raised to the power 2, is also read as '5 squared'
53, which is 5 raised to the power 3, is also read as '5 cubed'.
Similarly, 102 is read as '10 squared' and 103 is read as '10 cubed'.
If follows from the above discussion that for any rational number a, we have
| a × a | = | a2 (read as 'a' squared or 'a raised to the power 2') |
| a × a × a | = | a3 (read as a raised to the power 4 or the 4th power of a) |
| a × a × a × a | = | a4 (read as a raised to the power 4 or the 4th power of a) |
| a × a × a × a × a | = | a5 (read as a raised to the power 5 or the 5th power of a) |
| and so on. |
an is called the nth power of a and is also read as 'a raised to the power n'.
Note: It is evident from the above discussion that
a × a × a × b × b is written as a3b2 (read as a cubed into b squared)
a × a × b × b × b × b is written as a2b4 (read as a squared into b raised to the power 4)
If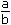 
is a rational number and n is a natural number, then
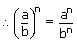
(−1)raised to any odd power = − 1 and
(−1)raised to any even power = 1
