Division of Objects
Groups of unequal size
The number of ways in which (p + q) objects can be divided into two unequal groups containing p and q objects respectively is:
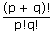
Proof:
Out of (p + q) objects 'p' objects can be selected in (p +
q)Cp ways.
Make them into a group and remaining into another
group.
(p + q)Cp
The number of ways in which (p + q + r) objects can be divided into three unequal groups containing p, q and r objects respectively is:
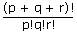
Proof:
Out of (p + q + r) objects 'p' objects can be selected in (p + q +
r)Cp ways.
Out of the remaining (q + r) objects, 'q' objects can be selected in (q +
r)Cr ways.
Remaining 'r' objects can be thought of as a
group.
∴ Total no. of ways of grouping
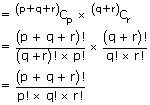
The number of ways in which 'n' distinct objects can be distributed to 'r' different persons = rn
Proof:
Instead of assuming 'r' different persons choosing 'n' different objects, it is better to
assume each object in 'n' objects chooses one person among 'r' persons.
First object chooses a person in 'r' ways
Second object chooses a person in 'r' ways
Third object chooses a person in 'r' ways
.
.
.
nth object chooses a person in 'r' ways
∴ Total no. of ways = rn
Group of equal size
The number of ways in which 'mn' different objects can be divided equally
into 'm' groups, each containing 'n' objects and the order of the groups is not important
is: 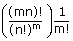 The number of ways in which 'mn' different objects can be divided equally into 'm' groups,
each containing 'n' objects and the order of the groups is important is:
The number of ways in which 'mn' different objects can be divided equally into 'm' groups,
each containing 'n' objects and the order of the groups is important is:
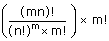
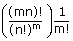
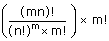
Proof:

| no. of ways of selecting 'n' objects for 1st group | = | mnCn |
| no. of ways of selecting 'n' objects for 2nd group | = | (mn – n)Cn |
| . | ||
| . | ||
| no. of ways of selecting 'n' objects for (m – 1)th group | = | (mn – (m – 2)n)Cn |
| no. of ways of selecting 'n' objects for mth group | = | (mn – (m – 1)n)Cn |
| ∴ Total no. of ways | = | mnCn × (mn – n)Cn ...... nCn |
| = | 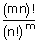
|
But 'm' groups are not ordered (There are 'm!' duplicacies for each
combination)
⇒ Total no. of ways = 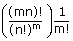
Identical objects into groups
Stars and bars method:
The number of ways of dividing 'n' identical objects among 'r' persons, each one of whom,
can receive zero or more objects is:
n + r – 1Cr –
1, where 0 ≤ r ≤ n.
Method - I
Proof:
It is a graphical aid for deriving combinatorial theorems.
Suppose 'n' identical objects are represented by stars.

Assume 'r – 1' bars are put among stars.
Consider gap between two successive bars as a bin. 'r – 1' bars put among n stars
create 'r' bins.
Number of stars between (k – 1)th and kth bar gives the no. of
stars contained in Kth bin.
The first bin contain stars left to that of first bar, similarly last bin (rth)
contains stars right to the last bar.
Example: Divide 8 stars into 5 bins.
One of the possible arrangements:
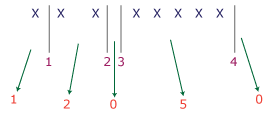
No. of stars in 5 bins are 1, 2, 0, 50 respectively.
'Stars and bars' arrangements have one – to – one correspondence with 'n
identical objects shared among r different persons'.
The stars in kth bin are assigned to kth person.
The number of
stars and bars is equal to n + r – 1.
Out of n + r – 1 objects,
'n' stars are similar and 'r – 1' bars are similar.
Total no. of ways of arranging = 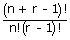
Method - II
The number of ways to divide 'n' identical objects among 'r' groups putting zero or more in a group
| The coefficient of xn in (x0 + x1 + . . . . + xn)r | = | The coefficient of xn in 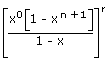
|
| = | The coefficient of xn in (1 – xn + 1)r(1 – x) – r | |
| = | The coefficient of xn in (1 – x) – r | |
| = | The coefficient of xn in 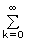 r + k – 1Ck xk
r + k – 1Ck xk |
|
| = | r + n – 1Cn (by putting k = n in r + k – 1Ck) | |
| = | n + r – 1Cr – 1 |
The number of ways of dividing 'n' identical objects among 'r' persons,
each one of whom, receives at least one item is
n – 1Cr –
1, where 1 ≤ r ≤ n
Proof:
Instead of arranging n + r – 1 stars and bars, 'r – 1' bars are arranged in 'n –
1' gaps between 'n' stars.
⨯ _ ⨯ _ ⨯ _ ⨯ _ .......⨯
'r – 1' spaces can be selected out of 'n – 1' spaces in (n – 1)Cr – 1 ways.
'r – 1' spaces can be selected out of 'n – 1' spaces in (n – 1)Cr – 1 ways.
This way we can ensure at least one star is there between two successive bars.
∴ No.of ways of dividing 'n' identical objects among r persons, each one of whom, receives at least one item
∴ No.of ways of dividing 'n' identical objects among r persons, each one of whom, receives at least one item
= (n – 1)Cr – 1
Method - II
The number of ways to distribute 'n' identical objects among r groups putting atleast one object in each
group
| The coefficient of xn in (x1 + x2 + . . . . + xn)r | = | The coefficient of xn in 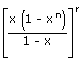 |
| = | The coefficient of xn in 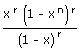 |
|
| = | The coefficient of xn – r in (1 – xn)r(1 – x)–r | |
| = | The coefficient of xn – r in (1 – x)–r | |
| = | The coefficient of xn – r in 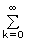 r + k – 1Ck xk r + k – 1Ck xk |
|
| = | r + (n – r) – 1Cn – r | |
| = | n – 1Cn – r | |
| = | n – 1Cr – 1 |