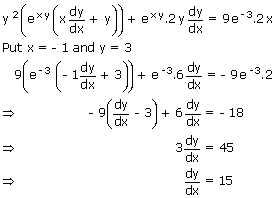Examples
Ex1:
Let f: (–1, 1) → R be a
differentiable function with f(0) = –1 and
f∣(0) = 1.
Let g(x) = [f(2f(x) + 2)]2. Then find g'(0).
Sol:
| Given g(x) | = | [f(2 f(x) + 2)]2 |
| ⇒ g'(x) | = | 2 f(2 f(x) + 2).f '(2 f(x) + 2).2f '(x) |
| Substituting x | = | 0, |
| ⇒ g'(0) | = | 2f(2 f(0) + 2).f '(2f(0) + 2).2f '(0) |
| = | 2f(0).f '(0).2f '(0) (∴ f(0) = –1 and f '(0) = 1) | |
| = | 2(–1)(1).2(1) = – 4 |
Ex2:
Find derivative of following functions ?
(i) y = ln3 tan2(x4)
(ii) exp (cos3(tan– 1x3)2)
(i) y = ln3 tan2(x4)
(ii) exp (cos3(tan– 1x3)2)
Sol :
(i) y = ln3 (tan2(x4))
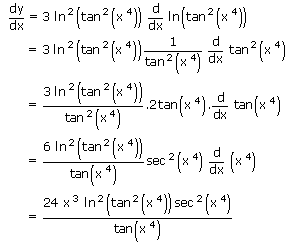
| (ii) y | = | exp (cos3(tan x3)2) |
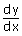 |
= | exp(cos3(tan x3)2).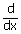 (cos3(tan x3)2)
(cos3(tan x3)2) |
| = | y.3 cos2(tan x3)2.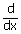 cos(tan
x3)2 cos(tan
x3)2 |
|
| = | 3y cos2(tan x3)2 (– sin(tan
x3)2).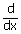 (tan
x3)2 (tan
x3)2 |
|
| = | – 3y cos2(tan x3)2 sin(tan x3)2) (2 tan (x3).sec2 x3).3x2 | |
| = | – 18y x2 cos2(tan x3)2.sin(tan x3)2 tan(x3) sec2 x3. |
Ex3:
Find 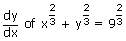 .
.
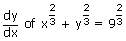 .
.Sol:
By differentiating both sides of the given equation with respect to 'x', we get:
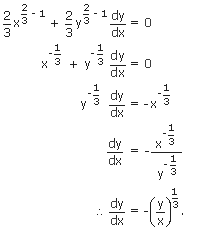
Ex4:

Sol:
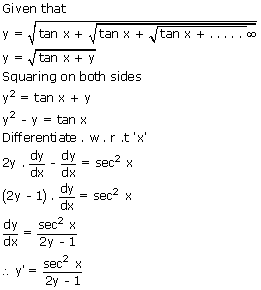
Ex5:
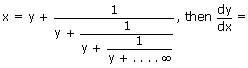
Sol:
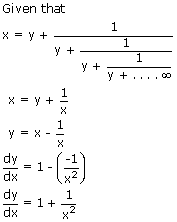
Ex6:
If y5 + xy2 + x3 = 4x + 3, then find 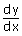 at (2, 1)
at (2, 1)
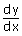 at (2, 1)
at (2, 1)
Sol:
y5 + xy2 + x3 = 4x + 3
differentiating w.r.t. x
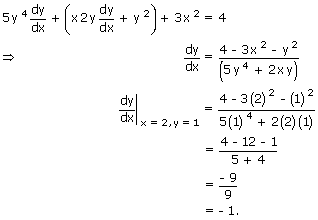
Ex7:
If y = x cosy + y cosx, find 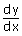
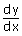
Sol:
Method 1:
Given y = x cosy + y cosx,
Differentiating both sides with respect to x, we get
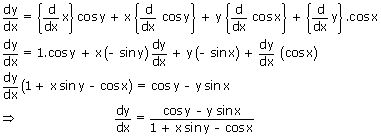
Method 2:
Shortcut method : y = x cosy + y cosx
Let f = x cosy + y cosx – y
⇒ 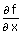 = cosy –
= cosy –
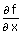 = cosy –
= cosy –y sinx and 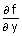 = – x
siny + cosx – 1
= – x
siny + cosx – 1
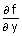 = – x
siny + cosx – 1
= – x
siny + cosx – 1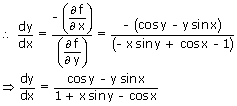
Ex8:
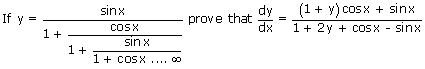
Sol:
Given function is y = 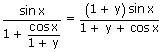
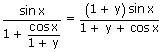
or y + y2 + y cosx = (1 + y)sinx
On differentiating both sides w.r.t. x we get
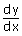 + 2y
+ 2y 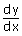 + y(–
sinx) +
cosx.
+ y(–
sinx) +
cosx.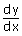 = (1 +
y)cosx +
= (1 +
y)cosx + 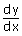 .sinx
.sinx⇒ 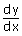 {1 + 2y + cosx
– sinx} = (1 + y)cosx + y sinx
{1 + 2y + cosx
– sinx} = (1 + y)cosx + y sinx
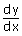 {1 + 2y + cosx
– sinx} = (1 + y)cosx + y sinx
{1 + 2y + cosx
– sinx} = (1 + y)cosx + y sinx⇒ 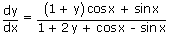
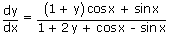
Ex9:
The equation y2exy = 9 e– 3x2
defines y as
a differentiable function of x. The value of 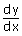 for x =
–1 and y = 3
for x =
–1 and y = 3
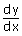 for x =
–1 and y = 3
for x =
–1 and y = 3Sol: