Examples
Ex1:
Which of the following pairs of triangles are
congruence? If they are congruent, write out the pairs of equal angles.
(i) ΔABC : AB = 3 cm, BC = 4 cm and CA = 2 cm
ΔDEF: DE = 2 cm, EF = 3 cm and FD = 4 cm
(ii) ΔPQR : PQ = 17 cm, QR = 15 cm, PR = 18 cm
ΔDEF: DE = 18 cm, EF = 17 cm and DF = 15 cm
Sol:
(i) In triangles, ABC and DEF, we have
AB = EF = 3 cm, BC = FD = 4 cm and CA = DE = 2 cm
So by SSS condition of congruence, we have
ΔABC ≅ ΔEFD
Since AB = EF, therefore angles opposite to these sides are equal.
⇒ ∠C = ∠D
Similarly, BC = FD ⇒ ∠A = ∠E
and, CA = DE ⇒ ∠B = ∠F
(ii) In In triangles, PQR and DEF, we have
PQ = EF = 17 cm, QR = FD = 15 cm and RP = DE = 18 cm
So by SSS condition of congruence, we have
ΔPQR ≅ ΔEFD
⇒ ∠P = ∠E, ∠Q = ∠F and ∠R = ∠D
Ex2:
In the following pairs of triangles, the lengths of
the sides are indicated along sides. By applying SSS condition, determine which are
congruent. State the result in symbolic form.
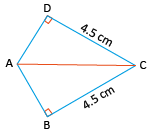
Sol:
In ΔABD and ΔEFC,
AB = FE = 5 cm (side)
AD = FC = 10.5 cm (side)
BD = CE = 7 cm (side)
SSS criterion is two triangles are congruent, if the three sides of triangles are
respectively equal to the three sides of the other triangle.
Therefore, SSS criterion of
congruence, ΔABD ≅ ΔFEC.
Ex3:
Which of the following pairs of triangles are
congruent ?
(i) ΔABC : AB = 2 cm, AC = 4 cm, ∠A = 40°
ΔXYZ : XZ = 2 cm, YZ = 4 cm, ∠Z = 40°
(ii) ΔPQR : PQ = 5 cm, PR = 6 cm, ∠P = 55°
ΔDEF : DE = 6 cm, EF = 5 cm, ∠D = 55°
Sol:
(i) In ΔABC and ΔXYZ, we have
AB = XZ = 2 cm, AC= YZ = 4 cm, ∠A = ∠Z = 40°
Thus, in ΔABC and ΔXYZ, the two sides and included angle of one triangle are
equal to two sides and corresponding included angle of the other.
So, by SAS congruence condition, we have
ΔABC ≅ ΔZXY.
(ii) In ΔPQR, the included angle between PQ and PR is ∠P
In ΔDEF, the included angle between DE and EF is ∠E
We have,
PQ = EF = 5 cm and PR = DE = 6 cm but ∠P ≠ ∠E
So, the given triangles are not congruent.
Ex4:
In figure, AB = AD and ∠BAC = ∠DAC.
(i) State in symbolic form the congruence of two triangles ABC and ADC that is true.
(ii) Complete each of the following, so as to make it true:
(a) ∠ABC
(b) ∠ACD
(c) Line segment AC bisect ______ And _____
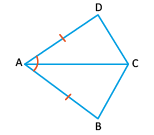
Sol:
(i) AB = AD (given)
∠BAC = ∠DAC (given)
AC = CA (common)
Therefore by SAS condition of congruency, ΔABC ≅ ΔADC
(ii) ∠ABC = ∠ADC (corresponding parts of congruent triangles)
∠ACD = ∠ACB (corresponding parts of congruent triangles)
Line segment AC bisects ∠A and ∠C.
Ex5:
Which of the following pairs of triangles are
congruent by ASA condition?
(i) 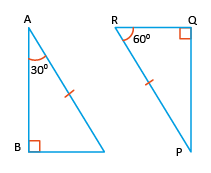

(ii) 


Sol:
(i) In ΔABC,
∠A + ∠B + ∠C = 180° (angle sum property)
∠C = 180° – ∠A – ∠B
∠C = 180° – 30° – 90° = 60°
In ΔPQR,
∠P + ∠Q + ∠R = 180° (angle sum property)
∠P = 180° – ∠R – ∠Q
∠P = 180° – 60° – 90° = 30°
∠BAC = ∠QPR = 30°
∠BCA = ∠PRQ = 60° and AC = PR (given)
Therefore, by ASA, ΔABC ≅ ΔPQR
(ii) We have only
BC = QR but none of the angles of ΔABC and ΔPQR are equal.
Therefore, ΔABC is not congruent to ΔPQR.