The below figure depicts a ball of mass 'm being dropped from a cliff of height H.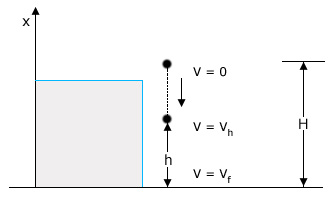

The TME of the ball, at height H, h and at the ground is

TME_H = mgH

TME_h = mgh + ½ mv_h²

TME₀ = ½ mv_f²

If work done is conservative, then we have,

TME_H = TME₀

mgH = ½ mv_f²

v_f = √(2gH)

In the case of a spring, the work done by the spring force is

W = kx dx = (kx_i² - kx_f²)/2

Thus the work done by the spring force depends only on the end points. It depends only on the initial and final positions. Thus, the spring force is a conservative force.

The potential energy of a spring is zero when it is at equilibrium position. If the spring is let to go, the speed of block increases from zero to a maximum value when it is at the origin. If the spring is let to go, the speed of block increases from zero to a maximum value when it is at the origin x = 0. The P.E decreases and K.E increases by the same amount. Since the spring is ideal, the energy is not converted into any other form like heat energy. As the block reaches the equilibrium position at x = 0, due to inertia of motion it overshoots and the spring is compressed by a. Then the position of block is x = -a. The P.E is once again maximum. Since the spring is compressed, the restoring force tries to bring the spring to the position x = 0. Thus the block is made to oscillate. Its energy changes from P.E to K.E, but total energy is always constant.

Total energy = Maximum P.E = Maximum K.E = ½ ka²

K.E at any position x = Total energy - P.E = ½ ka² - ½ kx²

⇒ K.E at any position x = ½ k(a² - x²)

i.e Kinetic energy is maximum at x=0.

The P.E cannot be greater than the total energy ½ ka². Because in that case K.E will become negative. This is not allowed. Thus the block goes up to +x₀ to -x₀ and not beyond that. Variation of P.E, K.E and T.E with displacement x is as shown in the figure below.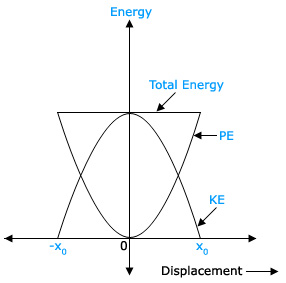

P.E and K.E varies as the square of displacement i.e x², so these graphs are parabolic. Total energy also depends on square of displacement x₀², but x₀ is constant. So total energy is a straight line parallel to X-axis.