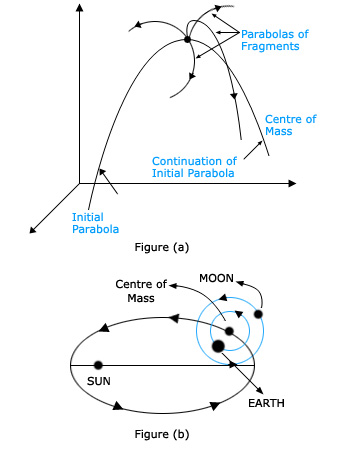
1. Explosion of a Cracker or a Shell: Initially the cracker is moving along a parabolic path. While in flight it explodes. Each fragment will follow its own parabolic path. But the center of mass of all the fragments will continue to be along the same parabolic path of the shell as before, because there was no external force and explosion is caused by internal force only (refer figure.a).
2. Motion of Earth-Moon System: Moon goes round the Sun in a circular orbit. The Earth goes round the Sun in elliptical order. It is more correct to say that the Earth and the Moon both move in circular orbits about their common center of mass describes an elliptical orbit round the Sun. Here Earth and Moon from a system and their gravitational force of attraction is an internal force. But Sun's attraction on both is an external force acting on their center of mass (refer figure.b).
3. Decay of radioactive nucleus: Consider a parent nucleus at rest. The total initial momentum is zero. Let it spontaneously decay into fragments caused by internal force only. So the final momentum of two fragments must be zero. Hence two fragments fly off in opposite directions; heavier fragment move with smaller velocity. But their center of mass will continue to be at rest, as the parent nucleus was at rest initially.
 Binary Stars
Binary Stars
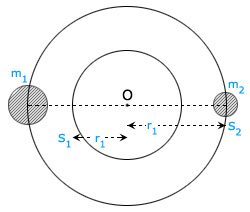
Binary stars (Double stars): Binary system consists of two particles undergoing accelerated motion, about their centre of mass. No external force acts on the system. But there will be internal forces, the adjacent figure shows a binary system consisting of two stars of masses m1, m2 gravitationally bound and separated by a distance r. They revolve around a common centre of mass O with a period T. Let r1 and r2 be their radii of revolution. From the definition of centre of mass
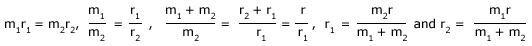
Let v1 and v2 be the speeds of revolution of the stars S1 and S2 respectively. Then v1 = 2Πr1/T and v2 = 2Πr2/T. The force of attraction between the two stars provides the centripetal force for m2,
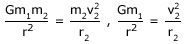 But
But 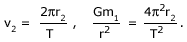
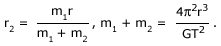
Knowing r, T, G, (m1+m2) can be calculated. Then the masses of the individual stars can be calculated using the equation m1 = [r2(m1+m2)] / r and m2 = [r1(m1+m2)] / r.
From this the luminosity of the stars and hence the distance of the binary stars from the earth can be estimated.