Consider a particle moving along a straight line with a variable speed. The position‐time graph is as graph (a) shown below.

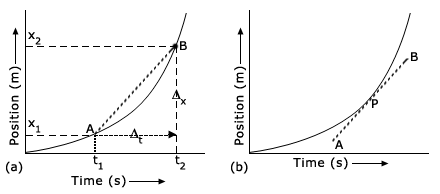
The particle has a velocity v₁ at point A(v₁ = x₁/t₁) and a velocity v₂ at the point B(v₂ = x₂/t₂)
The average velocity during the time interval Δt = t₂ – t₁ is v_av

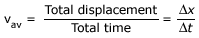
But Δx/Δt is the slope of the chord AB, which is the straight line joining the initial and final positions of the particle on the position time graph.

The instantaneous velocity is the velocity at a particular instant. For this we make Δt to become smaller and smaller. Then the points A and B will become closer and closer. When Δt tends to zero, the two points will coincide and the chord will become the tangent at that point. Hence the slope of the tangent AB to the curve at the point P on the position‐time graph gives the instantaneous velocity at that point [refer graph (b)].

The slope of the chord AB gives the average velocity and the slope of the tangent gives the instantaneous velocity.

If the particle travelled with uniform velocity then the position‐time graph would have been a straight line with a positive slope. In that case the slope of the chord and the slope of the tangent at any point would be equal. This means the average velocity is same as instantaneous velocity, provided the particle's velocity is uniform.

From the Displacement‐time graphs of a particle shown below, what conclusions can be drawn about the velocity of the particle?

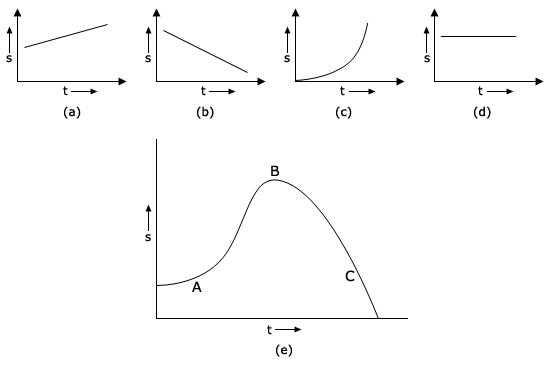
From the graph (a), the slope is constant and positive. The particle moves with the constant velocity.

From the graph (b), the slope is constant and negative. The particle moves with the negative constant velocity.

From the graph (c), the slope is variable and positive. the particle moves with variable velocity.

From the graph (d), the slope is zero. The particle is at rest.

From the graph (e), at the point A, the slope increases, the velocity increases, at B, the slope is zero, the body is at rest and at c, the slope is decreasing, the velocity is decreasing.