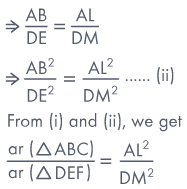EXAMPLES
Ex 1:
Prove that the ratio of the areas of two similar triangles is equal to
the ratio of the squares of their corresponding angle-bisector
segments.
Sol:
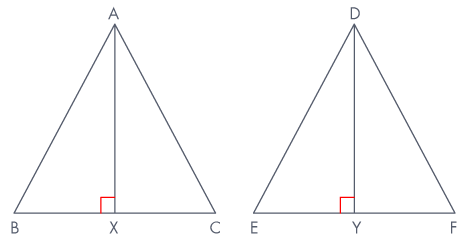
Given ΔABC ∼ ΔDEF in which AX and DY are the
bisectors of ∠A and ∠D respectively.
To prove


Proof:We know that ratio of the
areas of two similar triangles is equal to ratio of the squares of the
corresponding sides.
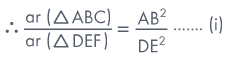
ΔABC ∼ ΔDEF
⇒ ∠A = ∠D
⇒
 ∠A =
∠A =
 ∠D
∠D
 ∠A =
∠A =
 ∠D
∠D
⇒ ∠BAX = ∠EDY
Now, in ΔABX and ΔDEY, we have:
∠BAX = ∠EDY and ∠B = ∠E [∵
ΔABC ∼ ΔDEF]
∴ ΔABX ∼ ΔDEY [By
AA-Similarity ]
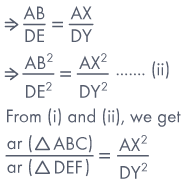
Ex 2:
Prove that the ratio of the areas of two similar triangles is equal to
the ratio of square of their corresponding altitudes.
Sol:
Given ΔABC ∼ ΔDEF, AL ⊥ BC and DM ⊥ EF.
To prove
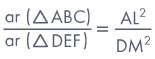
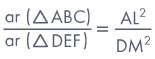
Proof:We know that the ratio of
the areas of two similar triangles is equal to the ratio of the
squares of the corresponding sides.
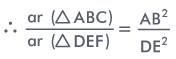
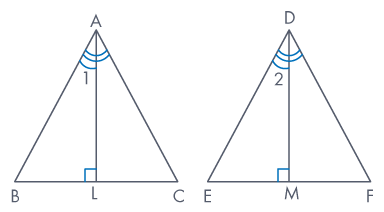
Now, in ΔALB and ΔDME, we have
∠ALB = ∠DME = 90° and ∠B = ∠E
[∵ ΔABC ∼ ΔDEF]
∴ ΔALB ∼ ΔDME [By
AA-similarity]