Examples
Ex 1:
A field in the form of a parallelogram has base 15 dam and altitude 8 dam. Find the cost of watering the field at the rate of 50 paise per square meter.
Sol:
| We have, | ||
| Base | = | 15 dam = (15 × 10) m = 150 m [∵ 1 dam = 10 m] |
| Altitude | = | 8 dam = (8 × 10) m = 80 m |
| ∴ Area of the field | = | (150 × 80) m2 |
| = | 12000 m2 | |
| The rate of watering the field | = | 50 paise per m2 |
| = | Rs.  per m2
per m2 |
|
| ∴ Cost of watering the field | = | Rs. 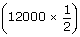 |
| = | Rs. 6000 | |
Ex 2:
The base of a parallelogram is thrice its height. If the area is 876 cm2, find the base and height of the parallelogram.
Sol:
| Let the height of the parallelogram be x cm. | ||
| Then, base | = | 3x cm. |
| ∴ Area of the parallelogram | = | (x × 3x) cm2 = 3x2 cm2. |
| But, the area of the parallelogram is given as 867 cm2. | ||
| ∴ 3x2 | = | 867 |
| ⇒ x2 | = | 289 |
| ⇒ x2 | = | 172 |
| ⇒ x | = | 17 |
| Thus, height | = | 17 cm and base = (3 × 17) cm = 51 cm. |
Ex 3:
The adjacent sides of a parallelogram are 10 m and 8 m. If the distance between the longer sides is 4 m. Find the distance between the shorter sides.
Sol:
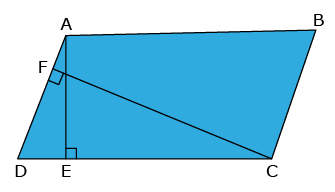
- Let ABCD is a parallelogram with side AB = 10 m and corresponding altitude AE = 4 m.
- The adjacent side AD = 8 m and the corresponding altitude is CF.
- We know that the area of a parallelogram = Base × Height.
- We have two altitudes and two corresponding bases.
- So, equating them we get:
- AD × CF = AB × AE
- 8 × CF = 10 × 4
- CF =
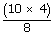 = 5 m
= 5 m - Hence, the distance between the shorter side is 5 m.