If the three sides of a triangle are 21cm, 20 cm, 13 cm then its area.
a = 21 cm, b = 20 cm, c = 13 cm

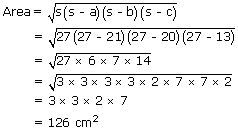
If 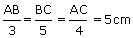 , then the semi-perimeter (s) =
, then the semi-perimeter (s) =
|
||
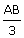
|
= | 5 |
| AB | = | 15 cm |
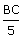
|
= | 5 |
| BC | = | 25 cm |
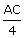
|
= | 5 |
| AC | = | 20 cm |
| AS a | = | 25 cm |
| b | = | 20 cm |
| c | = | 15 cm |
| (s)Semi-perimeter | = | 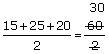 |
| s | = | 30 cm |
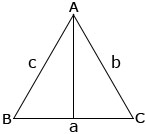
From the given figure find the length of AD(AD 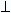 BC.)
BC.)
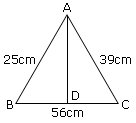
a = 25 cm, b = 39 cm, c = 56 cm
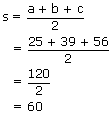
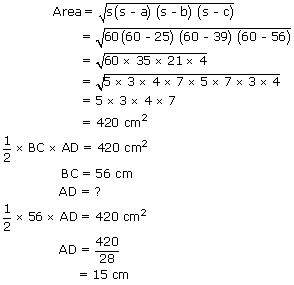
Using Heron's formula, find the area of an equilateral triangle of side a units.
We have: s =  (a + a + a) =
(a + a + a) =  a
a
| ∴ (s – a) | = | ( a – a) a – a) |
| = | 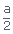 , ,
|
|
| (s – b) | = | ( a – a) a – a) |
| = | 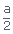 and
and |
|
| (s – c) | = | ( a – a) a – a) |
| = | 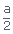
|
So, by Heron's formula, we have:
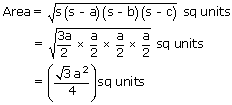
Hence, area of equilateral triangle of side a is 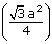 sq.
units.
sq.
units.
The base of an isosceles triangle measures 24 cm and its area is 192cm2. Find its perimeter.
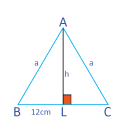
Let Δ ABC be an isosceles triangle and let AL ⊥ BC.
 × BC × AL = 192 cm2
× BC × AL = 192 cm2
⇒  × 24 × h = 192
× 24 × h = 192
⇒ h = (192/12) cm = 16 cm.
| Now, BL | = |  BC BC
|
| = | ( × 24) cm
× 24) cm |
|
| = | 12 cm and | |
| AL | = | 16 cm |
 |
||
| Hence, perimeter | = | (20 + 20 + 24) cm = 64 cm. |
The difference between the sides at right angles in a right-angled triangle is 14 cm. The area of of the triangle is 120cm2. Calculate the perimeter of the triangle.
Let the sides containing the right angle be x cm and (x – 14) cm.
| Then, the area of the triangle | = | [ × x × (x – 14)] cm2.
× x × (x – 14)] cm2. |
| But, area | = | 120 cm2 (given) |
∴  x(x
– 14) x(x
– 14) |
= | 120 |
| ⇒ x2 – 14x – 240 | = | 0 |
| ⇒ x2 – 24x + 10x – 240 | = | 0 |
| ⇒ x(x – 24) + 10(x – 24) | = | 0 |
| ⇒ (x – 24)(x + 10) | = | 0 |
| ⇒ x | = | 24[x = – 10 is not possible] |
| ∴ One side | = | 24 cm, other side = (24 – 14) cm = 10 cm |
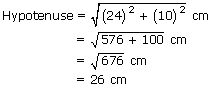 |
||
| ∴ Perimeter of the triangle = (24 + 10 +26 ) cm = 60 cm | ||
A triangular park ABC has side 120 m, 80 m, 50 m (see figure). A gardener Dhania has to put a fence all around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate Rs.20 per meter leaving a space 3 m wide for a gate on one side.
For finding area of the park, we have
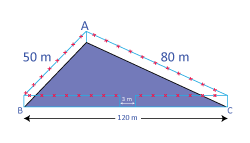
| 2s | = | 50 m + 80 m + 120 m |
| = | 250 m | |
| i.e s | = | 125 m |
| Now, s – a | = | (125 – 120) m |
| = | 5 m | |
| s – b | = | (125 – 80) m |
| = | 45 m | |
| s – c | = | (125 – 50) m |
| = | 75 m | |
| ∴ Area of the park | = | 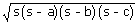 |
| = | 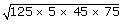 m2
m2 |
|
| = | 375√15 m2 | |
| Also, perimeter of the park | = | AB + BC + CA |
| = | 250 m | |
| ∴ Length of the wire needed for fencing | = | 250 m – 3 m (To be left for gate) |
| = | 247 m | |
| And so the cost of fencing | = | Rs.20 × 247 |
| = | Rs.4940 |