Examples
Ex1:
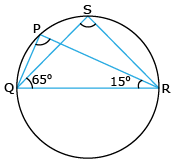
P, Q and R are three points on a circle with centre O such that ∠POQ = 30° and ∠QOR = 30°. If S is a point on the circle other than the arc PQR, find ∠PSR.
Sol:
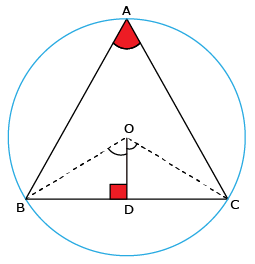
From the given figure
∠POR = ∠POQ + ∠QOR
= 30° + 30°
= 60°
We know that angle subtended by an arc at the centre is double the angle subtended by it any point on the remaining part of the circle.
∠PSR = ∠POR = (60°) = 30°
Ex2:
A chord of a circle is equal to the radius of the circle. find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Sol:
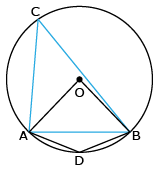
In ΔOAB,
AB = OA = OB = radius
∴ ΔOAB is an equilateral triangle.
Therefore, each interior angle of this triangle will be of 60°
∴ ∠AOB = 60°
∠ACB = ∠AOB = (60°) = 30°
In cyclic quadrilateral ACBD,
∠ACB + ∠ADB = 180deg; (opposite angle in cyclic quadrilateral)
∴ ∠ADB = 180° – 30° = 150°
Therefore, angle subtended by this chord at a point on the major arc and the minor arc are 30° and 150° respectively.
Ex3:
∠PQR = 65°, ∠PRQ = 15°, find ∠QSR?
Sol:
∠QPR = ∠QSR (angles in the same segment of the circle)
In ΔPQR,
∠QPR + ∠PQR + ∠PRQ = 180°
∠QPR + 65° + 15° = 180°
∠QPR = 180° – 80°
∠QPR = 100°
∠QSR = 100°
Ex4:
P, Q, R and S are four points on circle. PR and SQ are intersect at a point T such that ∠QTR = 120° and ∠TRS = 30°. Find ∠QPR?
Sol:

In ∠RST,
∠RST + ∠SRT = ∠RTQ (exterior angle)
∠RST + 30° = 120°
∠RST = 90°
∠QPR = ∠RST (angles in the same segment of a circle)
∴ ∠QPR = 90°
Ex5:
Prove that the angle in a semicircle is a right angle.
Sol:
Given AB is a diameter of a circle C(O, r) and ∠ACB is an angle in a semicircle.
To prove ∠ACB = 90°.
We know that the angle subtended by an arc at the centre is twice the angle formed. by it at any point on the remaining part of the circle.
∴ ∠AOB = 2 ∠ACB [Angle subtended by at O = 2 × angle formed by it at C].
⇒ 2∠ACB = ∠AOB = 180° [∵ ∠AOB is a straight angle].
⇒ ∠ACB = 90°.
Ex6:
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter, bisects the third side of the triangle.
Sol:
Given A Δ ABC in which AB = AC and a circle is drawn with AB as diameter, intersecting BC at D.
To prove BD = CD.
Construction Join AD.
We know that an angle in a semicircle is a right angle.
∴ ∠ADB = 90° ------------- (i)
Also, BDC being a straight line, we have:
∠ADB + ∠ADC = 180°
⇒ 90° + ∠ADC = 180° [Using (i)]
⇒ ∠ADC = 90°
Now, in Δ ADB and Δ ADC, we have:
AB = AC [given]
∠ADB = ∠ADC [each equal to 90°]
AD = AD [common]
Δ ADB ≅ Δ ADC [By SAS-congruence]
Hence, BD = CD [By cpct].
Ex7:
If O is the circumcentre of a ΔABC and OD ⊥ BC, prove that ∠BOD = ∠A.
Sol:
Given A ΔABC whose circumcentre is O and OD ⊥ BC.
To Prove ∠BOD = ∠A
Construction join OB and OC.
In the right-triangles Δ OBD and Δ OCD, we have
OB = OC [radii of the same circle]
OD = OD [Common]
∴ Δ OBD ≅ Δ OCD
⇒ ∠BOD = ∠COD [By RHS-congruence]
⇒ ∠BOD = ∠BOC
⇒ ∠BOD = ∠A [∵ ∠A = ∠BOC]