The weight of a body on a surface comes due to the reaction of a supporting surface, i.e., the Apparent weight of a body in a lift
Wapp = Reaction of supporting surface. Consider a person standing on a spring balance, or in a lift. The following situations are possible:
Case(i):
If the lift is at rest or moving with constant velocity then the person will be in translatory equilibrium. So, R = mg
∴ Wapp = mg [as Wapp = R]
or Wapp = W0[as W0 = mg = true weight]
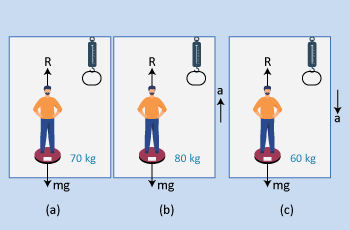
i.e., apparent weight (reading of balance) will be equal to the true weight.
Case(ii):
If the lift is accelerated up or retarding down with acceleration 'a' from Newton's II law we have
| R – mg | = | ma or R = m(g + a) |
| or Wapp | = | m(g + a) |
| = | 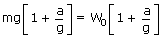 or Wapp > W0 or Wapp > W0 |
i.e., apparent weight(reading of balance) will be more than true weight.
Case(iii):
If the lift is accelerated down or retarding up with acceleration 'a' mg – R = ma i.e.,
| R | = | m(g – a) |
| or Wapp | = | m(g – a) [as Wapp = R] = mg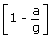 |
| i.e., Wapp | = | W0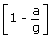 or Wapp < W0 or Wapp < W0 |
i.e., apparent weight(reading of balance) will be lesser than true weight.
Note:
If a > g, Wapp will be negative; negative weight will mean that the body is pressed against the roof of the lift instead of the floor (as the lift falls faster than the body) and so the reaction will be downwards, the direction of apparent weight will be upwards.
Case(iv):
If the lift is freely falling, Then a = g, so mg – R = mg i.e., R = 0. So, Wapp = 0
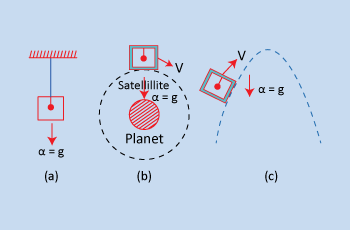
(a) Freely falling lift
(b) Satellite motion
(c) Projectile motion
i.e., the apparent weight of a freely falling body is zero. This is why the apparent weight of a body is zero, or the body is weightless if it is in
(i) a lift whose cable has broken,
(ii) orbiting satellite.