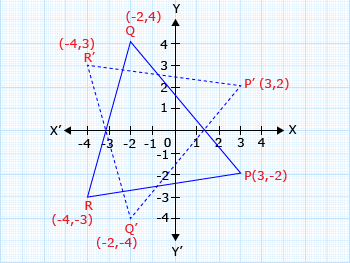
A triangle PQR has vertices P(3, – 2), Q(– 2, 4), R(– 4, – 3).

Draw the triangle PQR and its image under reflection in the x-axis.

Step I: Locate the points P, Q, R in the quadrants and join them.

Step II: Here x-axis is the line of reflection. So the reflection of the triangle will be P'Q'R' with the co-ordinates.

P(3, – 2) → P'(3, 2)

Q(– 2, 4) → Q'(– 2, – 4)

R(– 4, – 3) → R'(– 4, 3)

Step III: Plot the reflected vertices and join them.

Hence, triangle P'Q'R' is the reflection of the triangle PQR in the x-axis.

We observe that x-co-ordinate remains unchanged but y-co-ordinate is changed to its opposite sign, i.e, (a, b) → (a, – b)

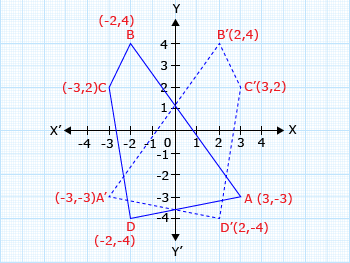
A quadrilateral ABCD with vertices A(3, – 3), B(– 2, 4), C(– 3, 2), D(– 2, – 4). Find the reflection in the y-axis.

Step I: Locate the points A, B, C, D in the quadrants and join them.

Step II: Here y-axis is the line of reflection. So the reflection of the quadrilateral will be A'B'C'D' with the co-ordinates.

A(3, – 3) → A'(– 3, – 3)

B(– 2, 4) → B'(2, 4)

C(– 3, 2) → C'(3, 2)

D(– 2, – 4) → D'(2, – 4)

Step III: Plot the reflected vertices and join them.

Hence, quadrilateral A'B'C'D' is the reflection of the quadrilateral ABCD in the y-axis.

We observe that y co-ordinate remains unchanged but x co-ordinate is changed to its opposite sign, i.e, (a, b) → (– a, b)

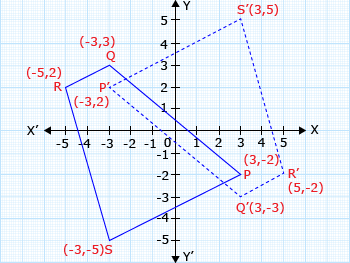
A quadrilateral PQRS with vertices P(3, –2), Q(– 3, 3), R(– 5, 2), R(–3, – 5). Find its reflection in the origin.

Since origin is the mid-point of a vertex and its image, both x and y co-ordinates will change their signs

i.e, (a, b) → (– a, – b).

Step I: Locate the points P, Q, R, S in the quadrants and join them.

Step II: Here origin is the point of reflection. So the reflection of the quadrilateral will be P'Q'R'S' with the co-ordinates.

P(3, –2) → P'(– 3, 2)

Q(– 3, 3) → Q'(3, – 3)

R(– 5, 2) → R'(5, – 2)

S(– 3, – 5) → S'(3, 5)

Step III: Plot the reflected vertices and join them.

Hence, quadrilateral P'Q'R'S' is the reflection of the quadrilateral PQRS in the origin.

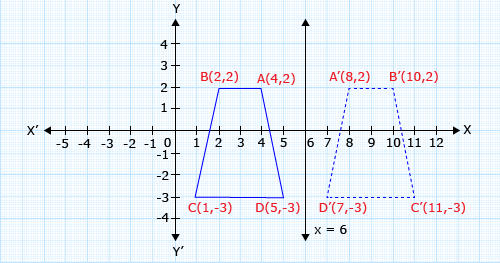
A trapezoid ABCD with vertices A(4, 2), B(2, 2), C(1, – 3), D(5, – 3). Find its reflection on a line x = 6.

Step I: Draw perpendicular segments from ABCD to line segment x = 6.

Step II: Locate A', B', C', D' so that line x = 6 is the perpendicular bisector of AA', BB', CC' and DD'.

A(4, 2) → A'(8, 2)

B(2, 2) → B'(10, 2)

C(1,– 3) → C'(11, – 3)

D(5, – 3) → D'(7, – 3)

Step III: Connect vertices A', B', C' and D'.

Hence, trapezoid A'B'C'D' is the reflection of the trapezoid ABCD in line x = 6.