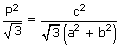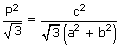Proofs
Product of the perpendiculars
The product of the perpendiculars from a point (α, β) to the pair of lines ax2 +
2hxy + by2 = 0 is given by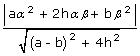 
Proof:
Let ax2 + 2hxy + by2 = 0 represent the lines.
l1x + m1y = 0 ----- (1) and
l2x + m2y = 0 ----- (2)
∴ (l1x + m1y) (l2x + m2y) =
ax2 + 2hxy + by2
⇒ l1l2 = a; m1m2 = b;
l1m2 + l2m1 = 2h
The length of the perpendicular from (α, β) to line (1) is
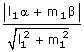
The length of the perpendicular from (α, β) to line (2) is
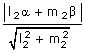
∴ The product of the perpendicular is
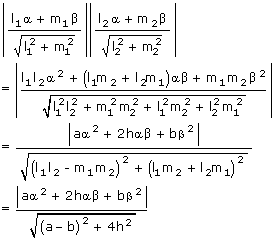
Area of a Triangle
The area of the triangle formed by ax2 + 2hxy + by2 = 0 and lx + my + n = 0 is
given by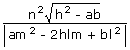 
Proof:
Let ax2 + 2hxy + by2 = 0 represent the lines.
l1x + m1y = 0 ----- (1) and
l2x + m2y = 0 ----- (2)
∴ (l1x + m1y) (l2x + m2y) =
ax2 + 2hxy + by2
⇒ l1l2 = a; m1m2 = b;
l1m2 + l2m1 = 2h
Let the given line be lx + my + n = 0 ----- (3)
Clearly the point of intersection of (1) & (2) is origin 'O'.
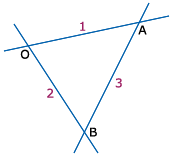
Let A be the point of intersection of (1) and (3).
| x | y | 1 | ||||
| m1 | O | l1 | m1 | |||
| m | n | l | m |
∴ 
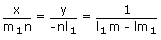
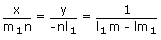
⇒ x =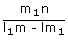 
,
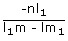
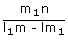y = 
,
y = 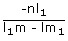∴ A =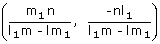 
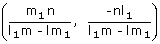
Similarly the point of intersection of (2) & (3) is
B =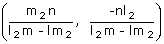 
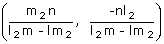
The area of ΔOAB
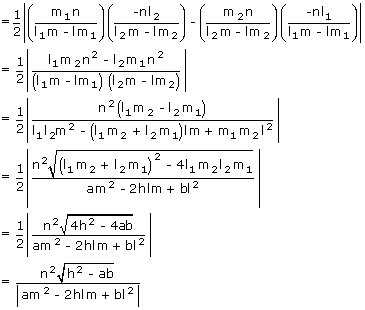
Area of equilateral triangle
The line ax + by + c = 0 and the pair of lines (ax + by)2 – 3(bx –
ay)2 = 0 form an equilateral triangle. Its area is given by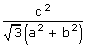 
sq. units
Proof:
Given that (ax + by)2 – 3 (bx – ay)2 = 0
⇒ [ax + by + √3 (bx – ay)] [ax + by – √3 (bx – ay)] = 0
⇒ [(a + √3 b)x + (– √3 a + b)y] [(a – √3 b)x + (√3 a + b)y]
= 0
∴ The equation represent the lines
(a + √3 b)x + (– √3 a + b)y = 0 ... (1)
(a + √3 b)x + (– √3 a + b)y = 0 ... (1)
(a – √3 b)x + (√3 a + b)y = 0 ... (2)
Let the given line be ax + by + c = 0 ... (3)
Let the given line be ax + by + c = 0 ... (3)
If A is an angle between (1) and (3), then
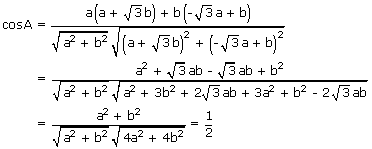
⇒ A = 60°
∴ The angles between (1) and (3) is 60°.
If B is an angle between (2) and (3), then
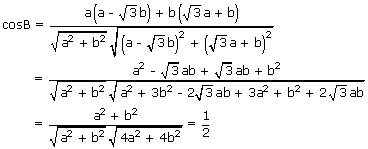
⇒ B = 60°
∴ The angles between (2) and (3) is 60°.
⇒ C = 60° (∵ A + B + C = 180°)
∴ The given lines form an equilateral triangle.
Since (1) and (2) are different lines it follows that the lines (1), (2), (3) form an equilateral
triangle.
The length of the altitude of the triangle, p
= The perpendicular distance from the
origin O to the line (3) =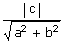 
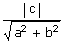
∴ Area of the triangle = 