Proof:
Let f(θ) = a cos θ + b sin θ
Also, let a = r sin α and b = r cos α.
Therefore we have
a2 + b2 = (r2 sin2 α) + (r2
cos2 α) and a/b = r sin α / r cos α
a2 + b2 = r2 (sin2 α + cos2
α) and a/b = tan α
r = 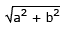 ---- (i) and tan α = a/b ---- (ii)
---- (i) and tan α = a/b ---- (ii)
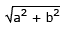 ---- (i) and tan α = a/b ---- (ii)
---- (i) and tan α = a/b ---- (ii)Substituting the values of a and b in f(θ), we have
f(θ) = r sin α cos θ + r cos α sin θ
f(θ) = r(sin α cos θ + cos α sin θ)
f(θ) = r sin (α + θ) ---- (iii)
Knowing that
– 1 ≤ sin (α + θ) ≤ 1 for all θ
and multiplying throughout by r, we have
– r ≤ r sin (α + θ) ≤ r for all θ
Using (i) & (iii), we have
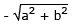 ≤ f(θ) ≤
≤ f(θ) ≤ 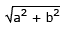 for all
θ
for all
θ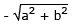 ≤ a cos θ + b sin θ ≤
≤ a cos θ + b sin θ ≤ 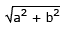 for all θ
for all θ
Hence, maximum and minimum values of a cos θ + b sin θ are 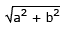 and
and
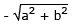 respectively.
respectively.
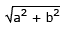 and
and
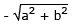 respectively.
respectively.