EXAMPLES
Ex 1:
2 sin2 30° – 3 cos2 45° + tan2 60°
Sol:
| Sol: Given 2 sin2 30° – 3 cos2 45° + tan2 60° | = |  |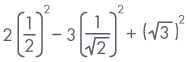
| = | 2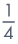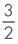. – 3. + 3 |
|
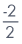| = | –  + 3 |
|
| = |  + 3 |
|
| = | - 1 + 3 | |
| = | 2 |
Ex 2:
If sin(A – B) =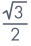 
, cos(A + B) = 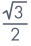, 0° < A + B ⩽ 30°, A > B. Find A and B.
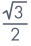, cos(A + B) = 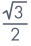, 0° < A + B ⩽ 30°, A > B. Find A and B. Sol:
Since sin(A – B) =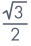
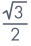
A – B = 60° ..... (i)
cos(A + B) =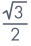
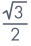
A + B = 30° ..... (ii)
By solving (i) and (ii)
A = 45° and B = –15°
A + B = 45° – 15° = 30°
Hence the given condition is satisfied.
Ex 3:
Evaluate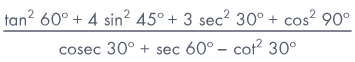 
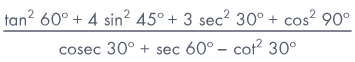
Sol:
Given that,
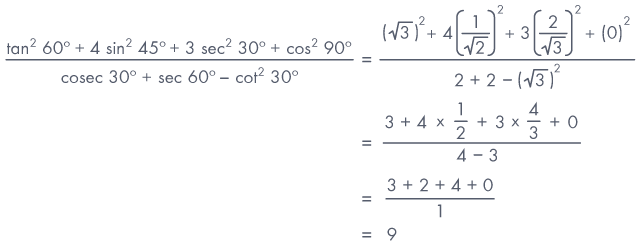
Ex 4:
Evaluate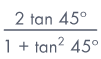 
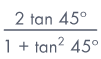
Sol:
Given that,
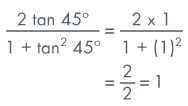
Ex 5:
In ΔABC, right-angled at B, AB = 6 cm and ∠ACB = 45°. Determine the length of the sides BC and AC.
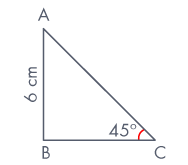
Sol:
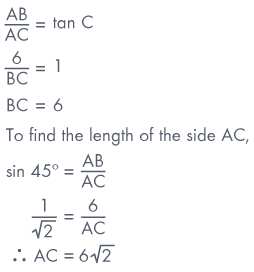
Ex 6:
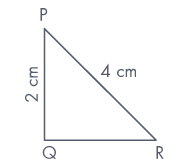
In ΔPQR, right-angled at Q, PQ = 2 cm and PR = 4 cm. Determine ∠QPR and ∠PRQ.
Sol:
 |
||
| Given PQ | = | 2 cm and PR = 4 cm |
∴  |
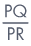= | sin R |
| sin R | = |  = |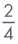
| ∠PRQ | = | 30° |
| ∠QPR | = | 60° |