Position of the image
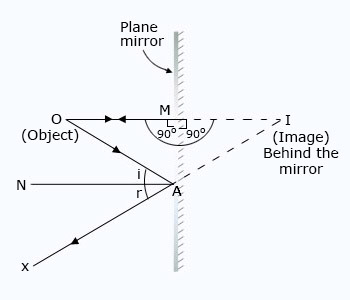
If we look into a plane mirror, we see the image of our face situated behind the mirror. Now, if we move backwards, the image also moves backwards in the mirror so that it is always at the same distance behind the mirror as our face is in front of the mirror. Thus, the image I in a plane mirror is as far behind the mirror as the object O is in front of it. In other words, the distance of the image from the plane mirror is equal to the distance of the object from the plane mirror.We will prove this fact by using the laws of reflection and simple geometry.
Consider an object O placed in front of a plane mirror (see Figure above). An incident ray of light OM coming from the object falls normally (or perpendicularly) on the mirror at point M and it is reflected back along the same path. Thus, OM represents the incident ray and MO represents the reflected ray. Let us now draw another incident ray OA which strikes the mirror at point A. It gets reflected along the path AX, making an angle of reflection NAX equal to the angle of incidence NAO (NA is the normal to the mirror at point A). Now, the first reflected ray is MO and the second reflected ray is AX. We produce the reflected rays MO and AX backwards by dotted lines. They appear to meet at point I (see Figure above). So, I is the virtual image of object O, We will now use this ray-diagram to prove that the distance of image from the plane mirror is equal to the distance of object from the mirror.
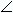 NAO =
NAO = 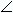 NAX ------ (1)
NAX ------ (1) MIA =
MIA = 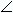 NAX ----- (2)
NAX ----- (2)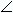 NAO =
NAO = 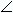 MIA ----- (3)
MIA ----- (3)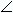 MOA =
MOA = 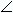 NAO ------ (4)
NAO ------ (4)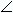 MIA =
MIA = 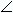 MOA ----- (5)
MOA ----- (5)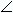 MIA =
MIA = 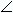 MOA (just proved)
MOA (just proved) IMA =
IMA = 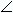 OMA (both are right angles)
OMA (both are right angles)Image of an extended object formed by a plane mirror
In below figure, let MM1 be a plane mirror infront of which an extended object AB is placed. From the points A and B of the object, rays of light travel in all directions. Let AP and AQ be two such rays incident on mirror from the point A which get reflected as PP' and QQ' respectively from the mirror. These reflected rays when produced backwards meet at the point A'. Thus A ' is the virtual image of the point A. Similarly from the point B of the object, BR and BS are the two incident rays on mirror which are reflected as RR' and SS' respectively and they meet at a point B ' when produced backwards. Thus, B' is the virtual image of the point B. Similarly, for the other points of the object AB, virtual image, are formed between A' and B'. Thus A 'B' is the virtual image of the object AB. It is erect and of size equal to that of the object.
Lateral inversion
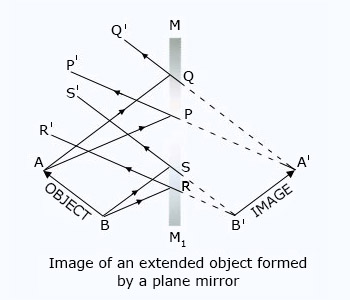
In our daily experience when looking in a mirror, we notice that a ring on the finger of the right hand appears to be in the finger of the left hand of our image and the pocket on the left appears to be on the right in the image.
The interchange of the left and right sides in the object and image is called the lateral inversion.
This type of inversion also occurs on the blotting paper used to dry ink while writing. The individual letter on the blotting paper can be read by seeing its image in a plane mirror. The letter P when seen in a plane mirror appears q as shown in figure.
Note that the lateral inversion of letters such as A, H, I, M, O, T, U, V, W, X and T, is not noticeable.
It is due to lateral inversion of the image formed in a plane mirror that it becomes difficult to read text on a page which is reflected by a plane mirror. The parting in our hair on the right appears to be on the left when seen in a mirror due to lateral inversion.