Pulley
1.
A pulley system has three pulleys in all and is 68% efficient. Calculate
(a) Mechanical advantage
(b) Effort required to lift a load of 816 N
(c) Resistance due to movable parts and friction of the pulley system
Sol:
| Velocity ratio (V.R.) | = | No.of pulleys = 3 | |
Knowing,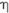 |
= | M.A./ V.R. | |
| M.A. | = | 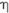 × V.R × V.R |
|
| = | (68/100) × 3 | ||
| = | 2.04 | ||
| Also, l/E | = | M.A. | |
| E | = | l / M.A. | |
| = | 816 N / 2.04 | ||
| = | 400N | ||
| Knowing, M.A | = | V.R. – (x/E) | . |
| x | = | E (V.R. – M.A.) | |
| = | 400 (3 – 2.04) | ||
| = | 384 N. |
2.
A pulley system lifts a load of 1000 N, by an effort of 320 N. If the resistance due to movable parts of machine and friction is 280 N, find
(i) Mech. advantage
(ii) Velocity ratio
(iii) Number of pulleys in system
(iv) Efficiency
Sol:
| (i) M.A. | = | Useful load/Effort |
| = | l / E | |
| = | 1000 N/320 N | |
| = | 3.125 | |
| (ii) Velocity Ratio | = | Ideal Mechanical Advantage |
| = | Total resistance overcome / Effort | |
| = | l + (x/E) | |
| = | 1000 N + (280 N / 320 N) | |
| = | 4 | |
| (iii) Number of pulleys | = | Velocity ratio = 4 |
(iv) Efficiency (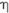 ) ) |
= | (M.A./V.R.) × 100 |
| = | (3.125/4) × 100 | |
| = | 78.13% |
3.
The radii of a differential pulley system are in ratio of 12:13. Calculate velocity ratio of system. If a load of 1tf is raised through a vertical height of 4 m, calculate
(i) distance through which effort is applied
(ii) effort required to lift load
Sol:
| Velocity ratio of differential pulley | = | (2R/R) – r |
| = | (2 × 13)/13 – 12 | |
| = | 26 | |
| (i) Velocity ratio | = | Distance through which effort moves/Distance through which load moves |
| 26 | = | Distance through which effort moves/4 m |
| ∴ Distance through which effort moves | = | 104 m |
| (ii) l / E | = | V.R. |
| ∴ 1 tf / E | = | 1000 kgf/E |
| = | 26 | |
| ∴ E | = | 1000 kgf/26 |
| = | 38.46 kgf. |