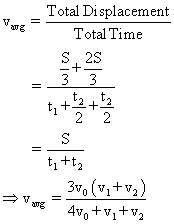A car travels 42 km at a uniform speed of 52 km/h and the next 42 km at a uniform speed of 32 km/h. Find its average speed
(i) First the car travels a distance of 42 kilometres at a speed of 52 kilometres per hour.
Let us find out the time taken by the car to travel this distance
| Here, Speed | = | 52 km/h |
| Distance | = | 42 km |
| And, Time | = | ?(To be calculated) |
| We know that,Speed | = | Distance/Time |
| So, 52 | = | 42/Time |
| And, Time | = | 42/52 hours |
| And, Time (t1) | = | 21/26 hours ------------- (1) |
(ii) Next the car travels a distance of 42 km at a speed of 32 km/h. We will also find out the time taken by the car to travel this distance.
| In this case : | ||
| Speed | = | 32 km/h |
| Distance | = | 42 km |
| And, Time | = | ? (To be calculated) |
| So, Speed | = | Distance/Time |
| And, 32 | = | 42/Time |
We can get the total time taken by the car for the whole journey by adding the above two time values t1 and t2 Thus,
| Total time taken | = | (21/26) + (21/16) hours |
| = | (168 + 273)/208 hours | |
| = | 441/208 hours ------------- (3) | |
| And, Total distance travelled | = | 42 km + 42 km |
| = | 84 km -------------- (4) | |
| Now, Average speed | = | Total distance traveller/Total time taken |
| = | 84 x (208/441) | |
| = | 17472/441 | |
| = | 39.62 km/h |
Thus, the average speed of the car for the whole journey is 39.62 kilometres per hour.
A train travels at a speed of 72 km/h for 0.62 h, at 45 km/h for the next 0.34 h and then at 84 km/h for the next 0.83 h. What is the average speed of the train ?
In this problem, first of all we have to calculate the distances travelled by train under three different conditions of speed and time
(i) In the first case, the train travels at a speed of 72 km/h for a time of 0.62 hours.
| Now, Speed | = | Distance/Time |
| So, 72 | = | Distance/0.62 |
| And, Distance | = | 72 x 0.62 |
| = | 44.64 km -------------- (1) |
(ii) In the second case, the train travels at a speed of 45 km/h for a time of 0.34 hours.
| Now, Speed | = | Distance/Time |
| So, 45 | = | Distance/0.34 |
| And, Distance | = | 45 x 0.34 |
| = | 15.3 km -------------- (2) |
(iii) In the third case, the train travels at a speed of 84 km/h for a time of 0.83 hours.
| Now, Speed | = | Distance/Time |
| So, 84 | = | Distance/0.83 |
| And, Distance | = | 84 x 0.83 |
| = | 69.72 km -------------- (3) |
| Total distance travelled | = | 44.64 + 15.3 + 69.72 |
| = | 129.66 km -------------- (4) | |
| And, Total time taken | = | 0.62 + 0.34 + 0.83 |
| = | 1.79 h | |
| We know that: Average speed | = | Total distance travelled / Total time taken |
| = | 129.66/1.79 | |
| = | 72.44 km/h |
A particle traversed on third of the distance with a velocity v0. The remaining part of the distance was covered with velocity v1 for half the time and with a velocity v2 for the remaining half of time. Assuming motion to be rectilinear, find the mean velocity of the particle averaged over the whole time of motion.
For AC; (S/3) = v0t1 &doublearrow; t1 = S/(3v0) ....(1)
For CB; (2S/3) = CD + DB
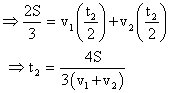
Since, average velocity is defined as
