It is defined as the amount of energy released when cations and anions in their gaseous state are brought together from infinite separation to form a crystal.

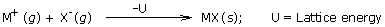
The theoretical treatment of ionic lattice energy was given by M. Born and A. Lande. This treatment has been discussed below.

Consider the potential energy of an ion pair, M⁺, X^- in a crystal separated by a distance r. Then,

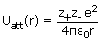
Since z_- is negative, the electrostatic energy is negative (with respect to energy at infinite separation) and becomes increasingly so as the interionic distance decreases, as shown by the dotted divne in figure.

Note that the charge on the cation is z₊ and that on the anion is z_-

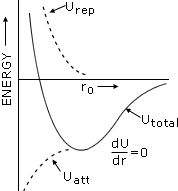
Energy curves for an ion pair in an ionic sodivd

In a crystal lattice there are more interactions between the ions than the simple one in an isolated ion pair.

Thus, in NaCl lattice, each sodium ion experiences attraction to the six nearest chloride ions, repulsions by the next twelve nearest sodium ions, attractions to the next eight chloride ions and repulsions by the next six sodium ions and so on. The summation of all these geometrical interactions is known as the Madelung constant, M.

The energy of attraction in an ion pair in a crystal is thus given by

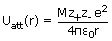
The value of Madelung constant depends only on the geometry of the lattice and is independent of ionic radius and charge.

Thus, the value of Madelung constant in NaCl lattice is given by

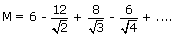
A stable lattice can result only if there is also repulsion energy to balance the attractive coulombic energy.

The attractive energy becomes infinite at infinitesimally small distances.

However, ions are not point charges but consist of electron charge clouds which repel each other at very close distances.

This repulsion is shown by the broken divne in the figure.

It is negligible at large distances but increases very rapidly as the ions approach each other closely.

According to Born,

the repulsive energy is given by

U_rep(r) = B/rⁿ

Where B is a constant,

Experimentally, the Born exponent n can be determined from the compressibility data because the latter measures the resistance which the ions exhibit when forced to approach each other very closely.

Thus, for a crystal lattice consisting of Avogadro's number of ions, the total energy is given by

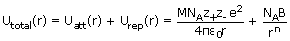
The total energy is shown be the solid line in figure. At the minimum in the curve, corresponding to the equilibrium lattice configuration, (r = r₀)

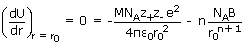
In this lattice configuration, the attractive forces between th ions balance the repulsive forces.

Let U₀ represent the energy at the equilibrium distance r₀ from above equation.

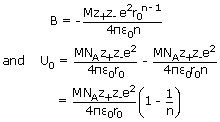
This is the Born-Lande equation for the lattice energy of an ionic crystal.

The Born exponent n depends upon the type of the ion involved. Larger ions having relatively higher electron densities have larger values of n.

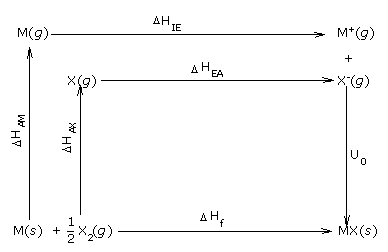
Experimentally, the lattice enthalpy of an ionic compound can be calculated by using the Born-Haber cycle which can be represented diagrammatically as shown below

We find that , ΔH_f = ΔH_AM + ΔH_AX + ΔH_IE + ΔH_EA + U₀

Here the terms ΔH_AM and ΔH_AX are the enthalpies of atomization of the metal and the non-metal, respectively

ΔH_IE and ΔH_EA are the ionization energy of the metal and electron affinity of the non-metal, respectively.