Consider a thin spherical shell of radius R with a positive charge q distributed uniformly on the surface. As the charge is uniformly distributed, the electric field is symmetrical and directed radially outward (positive charge) in all directions. The magnitude of electric field is the same at all points that are equidistant from the shell. All such points lie on a sphere. So the symmetry here is spherical symmetry. Hence we shall use a spherical Gaussian surface to find the electric flux and hence the magnitude of electric field at a point inside and outside of the charged shell.

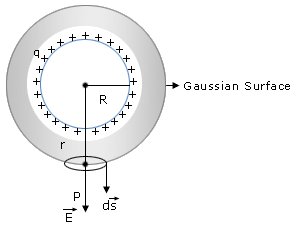
(a) Electric field outside the shell :

To find the magnitude of the electric field outside the charged shall, we evaluate the electric flux by using a spherical Gaussian surface of radius r(r > R) that is concentric with the shell.

Since the electric field

is everywhere perpendicular to the Gaussian surface, the angle between

and the elemental area

is 0°. Moreover, E has the same value at all points on the surface, since they are equidistant from the charged shell. Being constant, E can be taken out from the integral, and the total flux.

According to Gauss's law,

Q is the net charge in the Gaussian surface and is given as 'q'.

This is a surprising result, for it is the same as that for a point charge. Thus, the electric field outside a uniformly charged spherical shell is the same as if all the charge q were concentrated as a point charge at the centre of the shell.

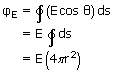
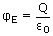
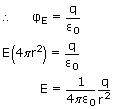
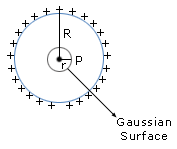
(b) Electric field inside the charged shell :

In this case we select a spherical Gaussian surface that lies inside the shell, concentric with it and with radius r(r < R). Inside the spherical shell, the electric field must also have spherical symmetry. So the electric flux through the Gaussian surface is

According to Gauss's law,

But the net charge enclosed by the surface is zero, since all the charge lies on the shell that is outside the Gaussian surface.

Therefore

Hence the electric field due to a uniformly charged spherical shell is zero at all points inside the shell.

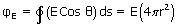
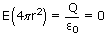
(c) Electric field on the surface of shell :

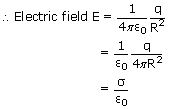
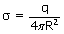In this case, the Gaussian surface is the shell itself i.e., r = R

where

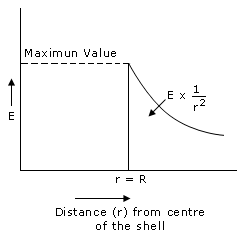
is the surface charge density on the shell.
The variation of electric field intensity with the distance from the center of a uniformly charged spherical shell is represented graphically below.

It can be observed that the electric field inside the shell is zero, maximum on the surface of the shell.
The electric field intensity varies inversely as the square of the distance from the centre, at a point outside the spherical shell.