Consider a thin plane infinite sheet having positive charge density σ. In order to find the electric field intensity at a point p, which is at a perpendicular distance r from the plane shell, we choose a closed cylinder of length
2r, whose ends have an area A as our Gaussian surface. The cylinder is arranged to pierce the sheet perpendicularly as shown.
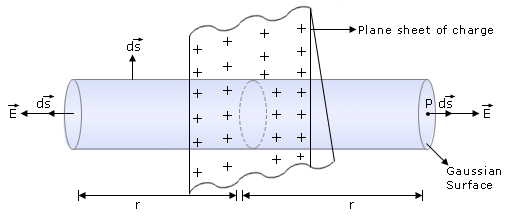
From the considerations of symmetry it is obvious that the electric field intensity is perpendicular to the sheet on both sides and directed away from the sheet ( charge is positive). Further
the magnitude of field intensity is same over the end caps.
charge is positive). Further
the magnitude of field intensity is same over the end caps.
 charge is positive). Further
the magnitude of field intensity is same over the end caps.
charge is positive). Further
the magnitude of field intensity is same over the end caps.The total electric flux through the Gaussian surface is the algebraic sum of flux due to cylindrical part and flux due to end caps of the Gaussian surface.Over the cylindrical part, the field lines are parallel to the surface. The angle
between
 and area element vector
and area element vector
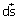 is 90°. As a result, no field lines cross this surface, giving zero flux through the cylindrical part. Therefore only end caps contribute to the electric flux. At the ends,
the normal component of
is 90°. As a result, no field lines cross this surface, giving zero flux through the cylindrical part. Therefore only end caps contribute to the electric flux. At the ends,
the normal component of  is equal to E.
is equal to E.
 and area element vector
and area element vector
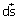 is 90°. As a result, no field lines cross this surface, giving zero flux through the cylindrical part. Therefore only end caps contribute to the electric flux. At the ends,
the normal component of
is 90°. As a result, no field lines cross this surface, giving zero flux through the cylindrical part. Therefore only end caps contribute to the electric flux. At the ends,
the normal component of  is equal to E.
is equal to E. Flux through Gaussian surface
Flux through Gaussian surface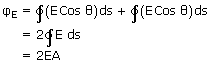
As σ is the charge per unit area in the plane sheet, the net positive charge within the Gaussian surface is σA.
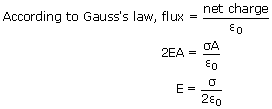
Therefore, the magnitude of the field does not depend on the distance from the plate. This is because as we move farther from the plane sheet of charge, more and more charges comes into our "field of view" and compensates the decrease
in field due to increase in distance. For a positively charged infinite sheet, the electric field points normally away from the plane and points normally into the sheet for a negatively charged plane sheet.
Electric field due to two infinite plane parallel sheets of charge:
Consider two infinite plane parallel sheets of charge A and B. Let σ1 and σ 2 be the uniform surface charge on A and B respectively.
Let σ 1 > σ2. The two sheets of charge divide the space into three regions, region I to the left of sheet A, II between the sheets and III to the right of sheet B
Let σ 1 > σ2. The two sheets of charge divide the space into three regions, region I to the left of sheet A, II between the sheets and III to the right of sheet B
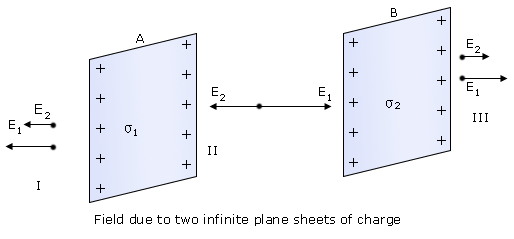
Let us assign positive sign to the electric field pointing from left to right and negative sign to the electric field pointing from right to left.In region I, the net electric field is given by
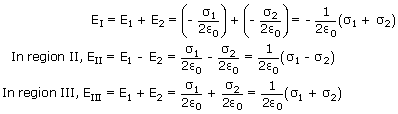
If the two sheets have equal and opposite uniform surface densities of charge i.e., σ 1 = σ and σ2 = – σ. Then
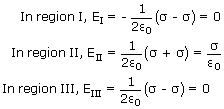
Therefore, the electric field between the sheets is constant i.e., a uniform field which is directed from the positive to negative sheet. While the field is zero on the outside of the two sheets. This arrangement is used for producing
uniform electric field.