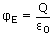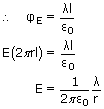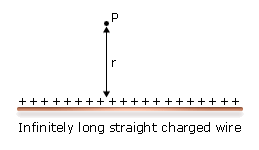
Consider an infinitely long thin wire with uniform linear charge density λ. That is, the charge per unit length is λ and this assumed to be the same for all points on the wire. From considerations of symmetry, we can say that
the electric field  is radially directed. The magnitude of the electric field is same at all those points which are equidistant from the wire. Let us find the electric field intensity
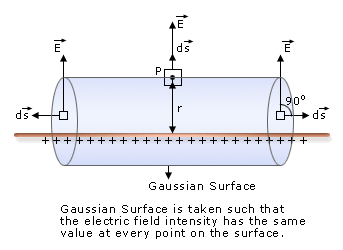
at any point P at a perpendicular distance r from the axis of the wire. A cylinder of radius r and arbitrary length l coaxial with the axis of the wire is chosen as the Gaussian surface.Since the Gaussian surface is a closed surface, this
cylinder is closed at each end by plane caps normal to the axis. The magnitude of
is radially directed. The magnitude of the electric field is same at all those points which are equidistant from the wire. Let us find the electric field intensity
at any point P at a perpendicular distance r from the axis of the wire. A cylinder of radius r and arbitrary length l coaxial with the axis of the wire is chosen as the Gaussian surface.Since the Gaussian surface is a closed surface, this
cylinder is closed at each end by plane caps normal to the axis. The magnitude of  is constant at all points on the surface of the cylinder, as those points are equidistant for the
wire and is normal to the surface (outward).
is constant at all points on the surface of the cylinder, as those points are equidistant for the
wire and is normal to the surface (outward).
 is perpendicular to the area element vector
is perpendicular to the area element vector  . Therefore, the electric flux through the caps is zero.
. Therefore, the electric flux through the caps is zero.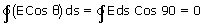
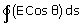 .
. and
and  is 0°, i.e., directed radically outward from the axis (∵ +vely charged)
is 0°, i.e., directed radically outward from the axis (∵ +vely charged)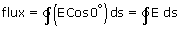
 is same at all points on the curved surface,
is same at all points on the curved surface,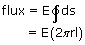
 times the net charge enclosed in the surface.
times the net charge enclosed in the surface.