One end of a 0.25 m long metal bar is in steam and the other in contact with ice. It 15 × 10– 3 kg of ice melts per minute, what is the thermal conductivity of the metal ? Given cross section of the bar is 7 × 10 – 4m2 and latent heat of ice is 80 cal/kg.
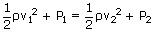
| Length of the rod x | = | 0.25 m |
| Area of cross section A | = | 7 × 10– 4 m2 |
| Temperature difference between two ends of the rod (T1 – T 2) | = | (100 – 0) |
| ; | = | 100° c |
| time t | = | 1 minute |
| ; | = | 60 s |
| If Q is the amount of heat required to melt 15 × 10 – 3 kg of ice, then | ||
| Q | = | m.L |
| Given latent heat of ice L | = | 80 Kcal/kg |
 Q Q |
= | 15 ×10– 3×80 ×1000 |
| ; | = | 1200 cal |
| coefficient of thermal conductivity k | = | 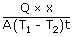 |
| ; | = | 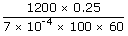 |
| ; | = | 71.4 cal s– 1 m– 1 °c– 1 |
The air in a room is at 25° c and outside temperature is 0° c. The window of the room has an area of 2m2 and thickness 2mm. Calculate the rate of loss of heat by conduction through window ? Thermal conductivity for glass is 1 Wm– 1degree– 1.
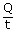
| Q | = | 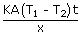 |
 Rate of loss Rate of loss 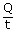 |
= | 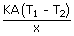 |
| k is Thermal conductivity of glass | = | 1 Wm– 1deg– 1 |
| A Area of the window | = | 2 m2 |
| T1 Temperature in the room | = | 25° c |
| T2Temperature outside the room | = | 0° c |
| x is thickness of the window | = | 2mm;= 2 × 10– 3 |
 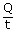 |
= | 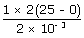 |
| ; | = | 25 × 103 w/s |
| ; | = | 25 kw/s |
One of the possible mechanisms of heat transfer in human body is conduction through body fat. Suppose that heat travels through 0.03 m of fat in reaching the skin, which has a total surface area of 1.7 m2 and a temperature of 34° c. Find the amount of heat that reaches the skin in half an hour, if the temperature at the body, interior is maintained at the normal value 37° c ? Thermal conductivity of body fat is k = 0.2 J/s.m.°c.
| Heat flow Q | = | 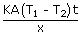 |
| Here k | = | 0.2 J/s.m.°c |
| A | = | area of the skin = 1.7 m2 |
| x | = | Thickness of fat = 0.03 m |
| T1 | = | Temperature at the body interior = 37° c |
| T2 | = | Temperature at the skin = 34° c |
| t | = | time taken for the heat to flow = 30 min= 1800 sec |
| Amount of heat flow that reaches the skin in half an hour | ||
| Q | = | 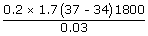 |
| Q | = | 6.1 × 104 J |
How ever, heat transfer via blood flow to the skin is more effective and has the added advantage that the body can vary the blood flow as needed.
The temperatures at the ends of a bar are 95° c at warmer end and 37° c at the cooler end. The length of the bar is 0.9 m. what is the temperature at a point that is 0.3 m from the cooler end of the bar ?
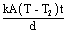
 T = T2 +
T = T2 + 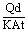
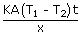
| T | = | T2 + 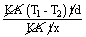 |
| T | = | T2 + 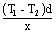 |
| ; | = | 37° + 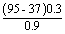 |
| T | = | 56.3° c |
Therefore the temperature is less than halfway between the temperature at warmer and cooler end.