Estimate the number of molecules we breathe in with a 1 liter breath of air?
We know that one mole of a gas contains 22.4 liters volume
| ∴ 1 liter | = | 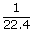 |
| ; | = | 0.045 moles |
| Number of molecules in liter of air | = | (NA) × number of moles |
| ; | = | 6.023 × 1023 × 0.045 |
| ; | = | 2.7 × 1022 molecules |
An automobile tyre is filled to a guage pressure of 250 k pa at 12°C. After a drive of 100 km, the temperature within the tyre rises to 42°C. Find the pressure in the tyre now?
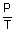 =
= 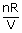
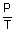 = constant
= constant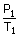 =
= 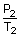
| ∴P1 | = | (250 k pa + 101 k pa) |
| ; | = | 351 k pa |
| T1 | = | 12°C |
| ; | = | 12 + 273 |
| ; | = | 285 k |
| T2 | = | 42°C |
| ; | = | 42 + 273 |
| ; | = | 315 k |
| The pressure after the drive P2 | = | 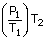 |
| ; | = | 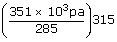 |
| P2 | = | 388 k pa |
| Subtracting the atmospheric pressure, | ||
| we get the gauge pressure | = | 388 × 101 |
| ; | = | 287 k pa |
Oxygen for patients in hospitals is kept in special tanks, at 65 atmospheres pressure and 288 k temperature in a separate room. The oxygen is pumped to the patients room, where it is maintained at 1 atm pressure and at 297 k. If oxygen occupies 1 m 3 of volume in the tanks, then what volume does it occupy at the condition's in the patient's room ?
| Pressure in the tank P1 | = | 65 atm |
| ; | = | 65 × 101.3 k pa |
| ; | = | 65 × 101.3 × 103 pa |
| Volume of oxygen in tank V1 | = | 1m3 |
| ; | = | 103 liters |
| Temperature of oxygen in tank T1 | = | 288 k |
| Pressure in the patients room P2 | = | 1 atm |
| ; | = | 101.3 kpa |
| Temperature maintained in the room T | = | 297 k |
| Volume of oxygen in patients room V | = | ? |
| From the ideal gas equation | ||
 |
= | 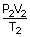 |
| V2 | = |  |
| ; | = | 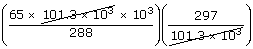 |
| ; | = | 67 × 103 litres |
Therefore volume of oxygen in the patients room is 67 m3
Calculate the temperature of the sun if density is 1.4 g/cm 3, pressure is 1.4 × 109 atm and average molecular weight of gases in the sun is 2. R = 8.4 J/mol k
| We know that PV | = | nRT |
| T | = | 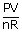 |
| But number of moles n | = | 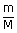 and M = molecular weight and M = molecular weight
|
| Density of gases ρ | = | 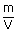 |
| ⇒ m | = | ρV |
| ∴ Number of moles n | = | 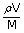 |
| ∴ Temperature of the sun T | = | 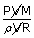 |
| ; | = | 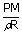 |
| Given P | = | 1.4 × 109 atm |
| = | 1.4 × 109 × 1.01 × 105 N/m2 | |
| = | 1.414 × 1014 pa | |
| Molecular weight M | = | 2 gm |
| ; | = | 2 × 10−3 kg |
| density of gases ρ | = | 1.4 g/cm3 |
| ; | = | 1.4 × 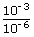 kg/m
3 kg/m
3 |
| ; | = | 1.4 × 103 kg/m3 |
| Substituting these values, Temperature of the sun is | ||
| T | = | 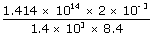 |
| ; | = | 24 × 107 k |
| At STP pressure P | = | 1.013 × 105 |
| Temperature T | = | 273 k |
| Number of moles n | = | 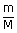 |
| m | = | 185 kg |
| M | = | molecular weight of N2 |
| = | 28 × 10−3 kg | |
| From the ideal gas equation PV | = | nRT |
| (a) Volume, V | = | 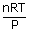 , R = 8.314 J/mol k. , R = 8.314 J/mol k.
|
| = | 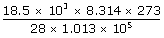 |
|
| V | = | 14.8 m3 |
| (b) Now additional 15 kg of nitrogen is added. | ||
| ∴Total mass | = | 18.5 + 15 |
| = | 33.5 kg | |
| Here volume and temperature are constant. | ||
So from the ideal gas equation
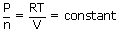 |
||
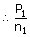 |
= | 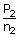 |
| Final pressure P2 | = | 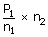 |
| Number of moles after adding 15 kg of N2 is | ||
| n2 | = | 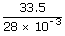 |
| ∴P2 | = | 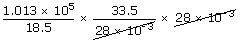 |
| ; | = | 1.83× 105 pa |