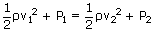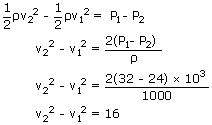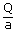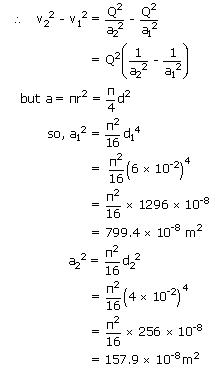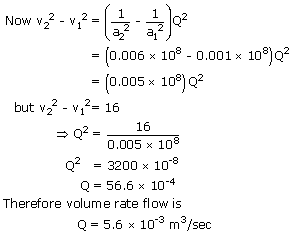Problems on Bernoulli's equation
Q1

Water enters a horizontal pipe of non-uniform cross-section with a velocity of 0.6m/s and leaves the other end with a velocity of 0.4m/s. At the first end, pressure of water is 1600N/m2. Calculate the pressure of water at the other end. Density of water = 1000 kg/m3?

Sol:

Bernoulli's equation for a horizontal pipe can be used to find the pressure at the second point of the pipe, which is

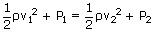
where, ρ is the density of water = 1000kg/m3
v1 is the velocity at first point = 0.6m/s
P1 is the pressure at first point = 1600N/m2
v2 is the velocity at second point = 0.4m/s
P2 is the pressure at second point = ?

Putting these values in the Bernoulli's equation,
Pressure of water at the other end of pipe is 1700 N/m2

Q2

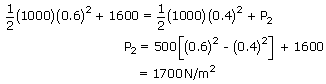
Calculate the minimum pressure required to force the blood from the heart to the top of the head (vertical distance 0.5m). Assume the density of blood to be 1040kg/m3. Friction is to be neglected ?

Sol:

Given vertical distance h2-h1 = 0.5m
density of blood ρ = 1040 kg/m3
minimum pressure required P1-P2 = ?
Applying Bernoulli's theorem,

Q3

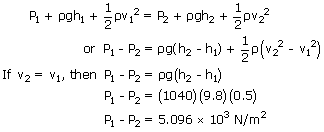
An airplane wing is designed so that the speed of the air across the top of the wing is 251m/s when the speed of the air below the wing is 225m/s. The density of air is 1.29kg/m3. What is the lifting force on a wing of area 24m 2?

Sol:

Speed of the air below the wing v1 = 225m/s
Speed of the air above the wing v2 = 251m/s
Density of the air ρ = 1.29kg/m3
Let P1 and P2 be the pressures below and above the wing respectively.

Then the change in pressure provides the net upward force.
According to Bernoulli's theorem

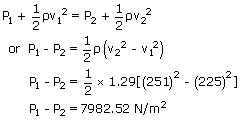
we know that pressure =
Net upward force = (pressure difference) Area of the wing
Given area of the wing = 24m2
So, force = 7982.52 × 24
= 1.92 × 105 N
Q4

Water is circulating through a closed system of pipes in a two floor apartment. On the first floor, the water has a gauge pressure of 3.4 × 10 5 pa and a speed of 2.1m/s. However, on the second floor, which is 4m higher, the speed of the water is 3.7m/s. The speeds are different because the pipe diameters are different. What is the gauge pressure of the water on the second floor?

Sol:

Gauge pressure in the first floor P1 = 3.4 × 105 pa.
Velocity of water in the first floor v1 = 2.1 m/s
Velocity in the second floor v2 = 3.7 m/s
Height difference between two floors (h2 - h1) = 4m
Gauge pressure in the second floor P2 = ?
Applying the Bernoulli's equation,
Pressure of water on the second floor is 3 × 105 Pa

Q5

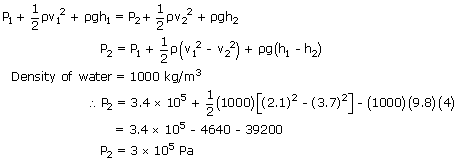
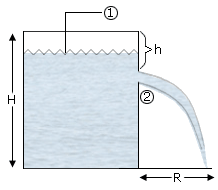
Water stands at a depth H in a large, open tank whose side walls are vertical. A hole is made in one of the walls at a depth h below the water surface. What is the distance R from the foot of the wall does the emerging stream strike the floor?

Sol:

We assume that the liquid behaves as an ideal fluid.
Therefore we can apply Bernoulli's theorem at points (1) and (2)

Since the pressures at points (1) and (2) is equal to the atmospheric pressure, P1 = P2
Now the Bernoulli's equation becomes

But given that h2 - h1 = h
If the tank is very large, the water level changes very slowly, and speed at point 1 can be set to zero

Now the emerging stream of water is just like a horizontal projectile, projected with velocity v = √(2gh)
The horizontal range of a projectile projected horizontally is

Q6

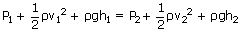
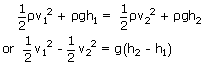
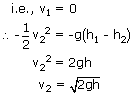
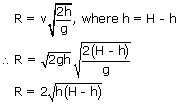
A 6cm diameter horizontal pipe gradually narrows to 4cm when water flows through this pipe at a certain rate, the gauge pressure in these two sections is 32 kpa and 24 kpa respectively. What is the volume rate of flow?

Sol:

Bernoulli's equation for horizontal pipe is
Given, P1 = 32kpa = 32 × 103pa
P2 = 24kpa = 24 × 103pa

But velocity v is related to the volume rate of flow by
Q = av (or) v =
Now the rate of flow is same at both the sections