Water flows through a pipe of internal diameter 20cm at the speed of 1m/s. What should the diameter of the nozzle be if the water is to emerge at the speed of 4m/s ?
| Given that, | ||
| The diameter of pipe at the entrance d1 | = | 20cm |
| radius r1 | = | 20cm |
| = | 0.1m | |
| Velocity of water while flowing into the system v1 | = | 1 m/s |
| Velocity of water at the exit v2 | = | 4 m/s |
| Radius of the pipe at exit r2 | = | ? |
| Area of the pipe a | = | πr2 |
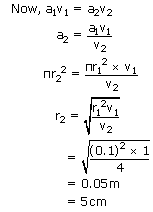
|
∴ Diameter of the pipe should be 10cm, so that the water can emerge at 4m/s speed.
A garden hose has an unobstructed opening with a cross-sectional area of 2.85 × 10-4 m2, from which water fills a bucket in 30 sec. The volume of the bucket is 8 × 10-3 m 3. Find the speed of the water that leaves the hose through the unobstructed opening and through an obstructed opening with half as much area ?
| we can obtain the speed of the water from the equation Q | = | av |
| where Q is the rate of flow, Q | = | 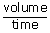
|
| a is the area of the hose cross section and v is the velocity of water | ||
| Now volume rate flow Q | = | 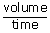
|
| = | 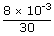
|
|
| Speed of the water through an unobstructed opening is v | = | 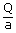
|
| = | 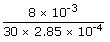
|
|
| = | 0.936 m/s |
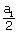
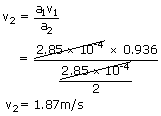
A patient who is recovering from surgery is being given fluid intravenously. The fluid has a density of 1030 kg/m3 and 9.5 × 10 -4m3 of it flows into the patient every six hours. Find the mass flow rate in kg/s ?
| Mass flow rate Q | = | 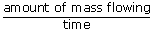
|
| Given, | ||
| Density of fluid | = | 1030 kg/m3 |
| volume of fluid | = | 9.5 × 10-4m3 |
| ∴ Mass of the fluid flowing | = | Density × Volume |
| = | 1030 × 9.5 × 10-4kg | |
| = | 9785 × 10-4kg | |
| Time taken to flow t | = | 6 hours |
| = | 6 × 60 × 60 sec | |
| ∴ Mass flow rate Q | = | 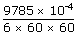
|
| = | 4.5 × 10-5kg/s |
| from the relation Q | = | 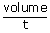
|
| Given volume of room/air | = | 120m3 |
| Time taken to replace the air | = | 20min |
| = | 20 × 60 sec | |
| ∴ Volume rate of flow Q | = | 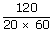
|
| = | 0.1 m3/s | |
| Now from the equation Q | = | av |
| where, a | = | area of the duct |
| v | = | speed of the air |
| If S is the length of a side of the duct(square), then | ||
| a | = | S2 |
| Q | = | S2v |
| S | = | 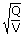
|
| For 3m/s speed of air, then length of the side is | ||
| S | = | 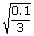
|
| = | 0.18 m | |
| For 5m/s speed, S | = | 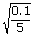
|
| = | 0.14m |
The aorta, which is the largest artery in the body; originating from the left ventricle of the heart and extending down to the abdomen, carries blood away from the heart at a speed of about 40cm/s and has a radius of approximately 1.1cm. The aorta branches eventually into a large number of tiny capillaries that distribute the blood to the various body organs. In a capillary, the blood speed is approximately 0.07cm/s and the radius is about 6 × 10-4cm. Treating the blood as an incompressible fluid, find the number of capillaries in the human body.
| Given that radius of aorta r | = | 1.1cm |
| Speed of the blood carried away from the heart v | = | 40cm/s |
| Rate of flow (volume) into the aorta Q | = | av |
| = | π r2 × v | |
| = | π × (1.1)2 × 40 | |
| Q | = | 152cm3/s |
| Rate of flow from the aorta | = | N(Rate of flow into each capillary) |
| Given that radius of a capillary | = | 6 × 10-4cm |
| and speed of the blood in capillary | = | 0.07cm/s |
| Then rate of flow into the capillary | = | πr2v |
| = | π(6 × 10-4)2 × 0.07 | |
| Q1 | = | 7.9 × 10-8cm3/s |
| Now Q | = | NQ1 |
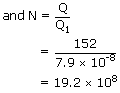
|