More Types of Functions
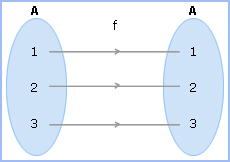
Identity function:
A function f: A → B is said to be an Identity function if f(x) = x for all x ∈ A that means it always returns the same value that is used as its input.
Identity function is denoted by I (first letter of Identity).
Constant function:
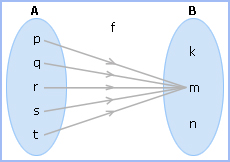
A function f: A → B is said to be a constant function if there is an element m ∈ B such that f(x) = m for all elements belongs to A.
That means the range of the function contains only one element.
Example:
Let f : A → B is a function defined as f(x) = m as x ∈ A, that is, f(p) = m, f(q) = m, f(r) = m, f(s) = m, f(t) = m.
So, 'f' is a constant function defined from A → B as f(x) = m for all x ∈ A.
Even function:
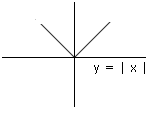
A function y = f(x) is said to be an even function, if f(– x) = f (x) ∀ x ∈ Domain (f).
For example: y = | x | is an even function since f(– x) = f (x) ∀ x ∈ Domain (f).
The graph of an even function is symmetric about y axis.
Odd function:
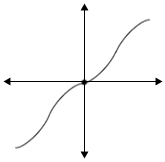
A function y = f(x) is said to be an odd function if f(– x) = – f (x), ∀ x ∈ Domain (f).
The graph of an odd function is symmetrical about the origin and passes through origin.
Equal functions:
Two functions f and g defined on the same domain D are said to be equal, if f(x) = g(x) for all x ∈ D.
For example: let f and g are two functions defined as f(x) = x + 2 for x ∈ N and g(x) = x + 2 for x ∈ N, then f and g are called equal functions.
Real function:
f : A → B such that A ⊆ R, then f is said to be a real variable function.
If f : A → B such that B ⊆ R, then f is said to be a real valued function.
If f : A → B and A, B are both subsets of the set of real numbers (R), then f is called a real function.
If f (x) is a real function, then 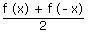 is always an even function and
is always an even function and 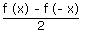 is always an odd function. But f(x) = 0 is both even and odd.
is always an odd function. But f(x) = 0 is both even and odd.
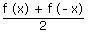 is always an even function and
is always an even function and 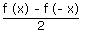 is always an odd function. But f(x) = 0 is both even and odd.
is always an odd function. But f(x) = 0 is both even and odd.