Proof of an exterior angle sum theorem
Theorem:The sum of measures of all the exterior angles at each vertex of a convex polygon is 360° (or) 4 right angles.
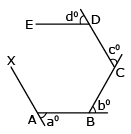
The sum of all the exterior angles of a convex polygon is 4 right angles
Given: A convex polygon ABCDEF.......of n sides, whose sides are produced in order, forming exterior angles a, b, c, d, etc.
To prove:a + b + c + d +...... = 4 right angles.
Statement Reason
1. A + a = 2 right angles.....(i) XA is a straight line.
2. B + b = 2 right angles, C + c = 2 right angles, D + d = 2 right angles and so on. Similarly, as (i)
3. (A + B + C + D + .....) + (a + b + c + d + .....) = 2n right angles. Polygon has n sides.
4. (2n – 4) right angles + (a + b + c + d......) = 2n right angles. The Sum of interior angles of a polygon of n sides is (2n – 4) right angles.
5. a + b + c + d...... = [2n – (2n – 4)] right angles = 4 right angles. From 4.
Hence, the sum of measures of all the exterior angles at each vertex of a convex polygon is 360° (or) 4 right angles.