Theorems on tangents of a circle
Theorem:
A tangent at any point of a circle is perpendicular to the radius through the point of tangency.
Given: A circle with the center O and PT is a tangent line to the
circle at the point P.
To prove: OP 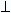 PT.
PT.
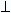 PT.
PT.Construction: Let Q be any point other than P, that means Q ≠ P on PT.
Join OQ.

Proof:
Since Q is any point other than P on PT.
 Q lies in the exterior of circle.
Q lies in the exterior of circle. OQ > OP.
OQ > OP.This shows that out of all segments that can be drawn from the center O to
any point on the line PT, OP is the shortest.
We know that the shortest segment that can be drawn from a given point to
a given line is the perpendicular from the given point to the given line.
Hence, OP 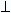 PT.
PT.
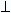 PT.
PT.Theorem:
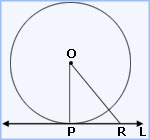
A line drawn through the end of a radius and perpendicular to it is a tangent to the circle.
Given: A circle of radius OP and a line L  OP.
OP.
 OP.
OP.To prove: Line L is a tangent to the circle at P.
Proof:
Take any point R, different from P on L.
Since OP  L, it
follows that among all the line segments joining O to a point
say R, on L, OP is the shortest.
L, it
follows that among all the line segments joining O to a point
say R, on L, OP is the shortest.
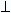 L, it
follows that among all the line segments joining O to a point
say R, on L, OP is the shortest.
L, it
follows that among all the line segments joining O to a point
say R, on L, OP is the shortest. OP < OR, i.e., OR> OP
for all R
OP < OR, i.e., OR> OP
for all R  the line
L.
the line
L. R lies outside the
circle for every point R on L.
R lies outside the
circle for every point R on L.This shows that the line 'L' meets the circle at only one point or we can say
that Line 'L' passes through two coincident points on the circle at P.
Therefore, L is a tangent to the circle at P.
Theorem:
The lengths of two tangents drawn from an external point to a circle are equal.
Given: Two tangents AP and AQ drawn from a point A to a circle C(O, r).
To prove: AP = AQ
Construction: Join OP, OQ and AO.

Proof:
Since AP and AQ are tangents to the circle at points P and Q.
 OP
OP 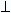 AP and OQ
AP and OQ 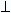 AQ.
AQ.
Now in right–angled triangles APO and AQO,
OP = OQ . . . . ( OP,
OQ are radii of the same circle).
OP,
OQ are radii of the same circle).
 OP,
OQ are radii of the same circle).
OP,
OQ are radii of the same circle).OA = OA . . . . ( OA
is common side for triangles APO, AQO).
OA
is common side for triangles APO, AQO).
 OA
is common side for triangles APO, AQO).
OA
is common side for triangles APO, AQO).So by R.H.S property, triangles APO and AQO are congruent triangles.
Hence, AP = AQ.