Proof of an interior angle sum theorem
Theorem 1:The sum of measures of all the interior
angles of a convex polygon of 'n' sides is (n – 2)180° (or) (2n – 4) right
angles.
Given: A convex polygon ABCDEF . . . . of n sides.
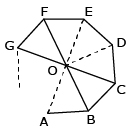
To prove: the Sum of all interior angles of the polygon = (2n – 4) right angles.
Construction: Take any point O inside the polygon and join OA, OB, OC, OD, OE ....etc.
Proof:
Polygon ABCDEF . . . . has been divided into n triangles, namely
OAB, OBC, OCD, ODE, etc.Sum of all the angles of n triangles = 2n right angles ...........(i)
(
Sum of all angles of one triangle = 2 right angles)
Sum of all angles of one triangle = 2 right angles) 
Sum of all interior angles of the polygon + Sum of all angles around O = 2n right angles (From (i))Moreover, we have the sum of all angles around O = 4 right angles.
( Sum of all angles around a point = 4 right angles.)
Sum of all angles around a point = 4 right angles.)Thus, the Sum of all interior angles of the polygon + 4 right angles = 2n right angles.
Sum of all interior angles of the polygon = (2n – 4) right angles. Hence, the sum of all interior angles of a polygon of n sides = (2n – 4) right angles.