Find common difference in the A.P. 21, 25, 29, 33, . . .
Given A.P. is 21, 25, 29, 33, . . .
| ⇒ t1 = 21, t2 | = | 25..... |
| We know that common difference d | = | tn – tn – 1 |
| ⇒ d | = | t2 – t1 |
| = | 25 - 21 = 4 |
Common difference for the A.P. 21, 25, 29, 33, . . . is 4.
Find the 12th term of the A.P. 5, 8, 11, 14, 17, . . . .
Given A.P. is 5, 8, 11, 14, 17......
| ⇒ t1 = 5, t2 | = | 8, . . . . |
| ⇒ d | = | t2 – t1 = 8 – 5 = 3 |
| ∴ a = 5, d | = | 3 |
| We know that nth term | = | a + (n – 1)d |
| 12th term | = | 5 + (12 - 1)(3) |
| = | 5 + 33 | |
| = | 38 |
Find the 18th term of the A.P. 18, 11, 4, – 3, – 10, . . . .
Given A.P. is 18, 11, 4, – 3, – 10, . . . .
| ⇒ t1 | = | 18, t2 = 11 , . . . . |
| ⇒ d | = | t2 – t1 = 11 – 18 = – 7 |
| ∴ a = 18, d | = | – 7 |
| We know that nth term | = | a + (n – 1)d |
| 18th term | = | 18 + (18 – 1)(– 7) |
| = | 18 – 119 | |
| = | 101 |
Write an A.P. whose first term is 8 and common difference is 3.
Given first term = 8, common difference = 3
We know that if a is the first term and d is the common difference, then
the arithmetic progression is a, a + d, a + 2d, a + 3d, . . .
| Here, a = 8, d | = | 3 |
| So, the required A.P. | = | 8, [8 + 3], [8 + 2(3)], [8 + 3(3)], [8 + 4(3)], . . . |
| = | 8, 11, 14, 17, 20, . . . . |
Write an A.P. whose first term is 5 and common difference is – 2
Given first term = 5, common difference = – 2
We know that if a is the first term and d is the common difference, then
the arithmetic progression is a, a + d, a + 2d, a + 3d, . . .
| Here, a = 5, d | = | – 2 |
| So, the required A.P. | = | 5, [5 + (– 2)], [5 + 2(– 2)], [5 + 3(– 2)], . . . |
| = | 5, 3, 1, – 1, . . . |
Write an A.P. whose first term is 2 and common difference is – 2/3
Given first term = 2, common difference = – 2/3
We know that if a is the first term and d is the common difference, then
the arithmetic progression is a, a + d, a + 2d, a + 3d, . . .
a = 2, d = – 2/3
So, the required A.P.
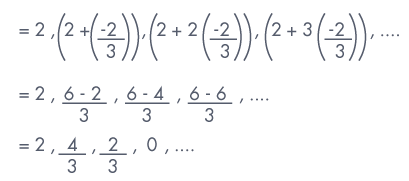
Write an A.P. whose first term is 6/5 and common difference is 1.
Given first term = 6/5, common difference = 1
We know that if a is the first term and d is the common difference, then
the arithmetic progression is a, a + d, a + 2d, a + 3d, . . .
Here, a = 6/5, d = 1
So, the required A.P.
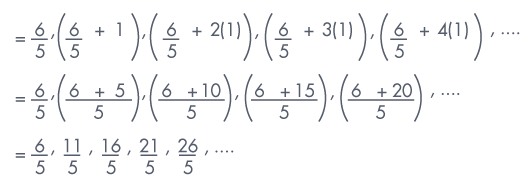
Determine the A.P. whose first term is – 8 and 16th term is 52.
| ⇒ a | = | – 8, t16 = 52 |
| ⇒ t16 | = | a + (16 – 1)d = a + 15d |
| ∴ 52 | = | – 8 + 15d [∵ t16 = 52, a = – 8] |
| ⇒ 15d | = | 60 |
| ⇒ d | = | 4 |
| We know that if a is the first term and d is the
common difference, then the arithmetic progression is a, a + d, a + 2d, a + 3d . . . . |
||
| a = – 8, d | = | 4 |
| So, the required A.P. | = | – 8, [(– 8) + 4], [(– 8) + 2(4)], [(– 8) + 3(4)], [(–8) + 4(4)], . . . . |
| = | – 8, – 4, 0, 4, 8, . . . | |
If the 8th term of an A.P. is 46 and the 19th term is 112, then find 14th term.
Let a be the first term and d be the common difference. Then,
| t8 | = | a + 7d, t19 = a + 18 d |
| Given, t8 | = | 46 , t19 = 112 |
| ⇒ a + 7d | = | 46 ...(i) |
| a + 18d | = | 112 ....(ii) |
| By solving (i) and (ii) we can find a, d values | ||
| ∴ From equation (i) we can write a | = | 46 – 7d |
| Substitute this 'a' value in equation (ii) | ||
| ⇒ [46 – 7d] + 18d | = | 112 |
| ⇒ 11d | = | 112 – 46 |
| ⇒ 11d | = | 66 |
| ⇒ d | = | 6 |
| Substitute this 'd' value in equation (i) | ||
| ⇒ a + 7d | = | 46 |
| ⇒ a + 7(6) | = | 46 |
| ⇒ a + 42 | = | 46 |
| ⇒ a | = | 46 – 42 |
| ⇒ a | = | 4 |
| ∴ finally, a | = | 4 , d = 6 |
| Now, we have to find 14th term, i.e., t14 | ||
| ⇒ t14 | = | a + 13d |
| = | 4 + 13(6) [∴ a=4,d=6] | |
| = | 4 + 78 | |
| = | 82 | |
Find the first negative terms of the sequence:
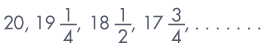

Thus 28th term of the given sequence is the first negative term.